题目内容
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.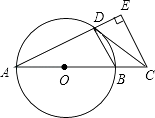
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
【答案】
(1)
证明:连接OD,
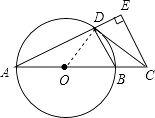
∵CD是⊙O切线,
∴∠ODC=90°,
即∠ODB+∠BDC=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ODB+∠ADO=90°,
∴∠BDC=∠ADO,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A;
(2)
解:∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∵∠BDC=∠A,
∴∠A=∠DCE,
∵∠E=∠E,
∴△AEC∽△CED,
∴ ![]() ,
,
∴EC2=DEAE,
∴16=2(2+AD),
∴AD=6.
【解析】本题考查了切线的性质,相似三角形的判定和性质,平行线的性质,熟练掌握切线的性质是解题的关键.(1)连接OD,由CD是⊙O切线,得到∠ODC=90°,根据AB为⊙O的直径,得到∠ADB=90°,等量代换得到∠BDC=∠ADO,根据等腰直角三角形的性质得到∠ADO=∠A,即可得到结论;(2)根据垂直的定义得到∠E=∠ADB=90°,根据平行线的性质得到∠DCE=∠BDC,根据相似三角形的性质得到 ![]() ,解方程即可得到结论.
,解方程即可得到结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目