题目内容
【题目】综合与实践探究几何元素之间的关系
问题情境：四边形ABCD中，点O是对角线AC的中点，点E是直线AC上的一个动点（点E与点C，O，A都不重合），过点A，C分别作直线BE的垂线，垂足分别为F，G，连接OF，OG.
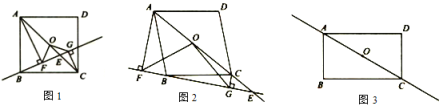
（1）初步探究：
如图1，已知四边形ABCD是正方形，且点E在线段OC上，求证
；
（2）深入思考：请从下面A，B两题中任选一题作答，我选择_______题.
A.探究图1中OF与OG的数量关系并说明理由；
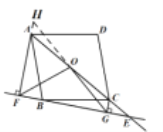
B.如图2，已知四边形ABCD为菱形，且点E在AC的延长线上，其余条件不变，探究OF与OG的数量关系并说明理由；
（3）拓展延伸：请从下面AB两题中任选一题作答，我选择_______题.
如图3，已知四边形ABCD为矩形，且
，
.
A.点E在直线AC上运动的过程中，若
，则FG的长为________.
B.点E在直线AC上运动的过程中，若
，则FG的长为________.
【答案】（1）见解析；（2）A. 
，理由见解析；B. . 理由见解析；（3）A.
B.
或
【解析】
（1）根据题意，AF⊥BE，CG⊥BE，
，
，则
，利用AAS证明
，即可得到答案；
（2）A．由（1）知
，
，然后得到OB=OA，由
，得到
，即可得到OF=OG；
B．延长GO交FA的延长线于点H，找到条件，证明
，然后得到OH=OG=OF；
（3）A．根据矩形的性质，得到△ABO是等边三角形，然后得到∠ABF=30°，则
，由勾股定理，求出BF和BG的长度，即可得到FG.
B．根据题意，由
，由两种情况，要进行分类讨论；结合矩形的性质，得到△AFB和△BCG是等腰直角三角形，利用三角函数值，求出BF和BG的长度，然后求出FG的长度即可.
（1）证明：∵四边形ABCD是正方形，
∴，
，
∴，
∵
，
，
∴
，
∴，
∴，
∴，
∴；
（2）A.解： ；
理由如下：如图1，连接OB，
由（1）知，，，
∵点O是AC的中点，
∴
，
，
∴
，
∴
，
∵
，
∴
，
∴，
∴，
∴；
B.解：.
理由如下：延长GO交FA的延长线于点H，
∵，，
∴
，
∴
，
∴
，
，
∵点O是AC的中点，
∴
，
∴，
∴
，
∴
，
∵
，
∴
，
∴ ；
（3）A、解：如图：连接OB，
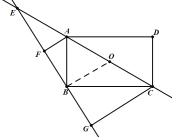
在直角三角形ABC中，OA=OB=OC，
∵∠BAC=60°，
∴△ABO是等边三角形，
∴∠ABO=60°，
∵BF=BG，
∴点B是FG的中点，
∴OB∥AF，
∴∠BAF=60°，
∵∠AFB=90°，
∴∠ABF=30°，
∴
，
∴
，
∴BG=
，
∴FG=
；
故答案为：.
B．解：①如图，OF∥BC，则OF⊥AB，
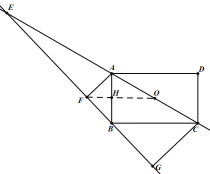
∵点O为AC中点，
∴点H为AB的中点，即AH=BH，
∴△ABF是等腰三角形，则AF=BF，
∵∠AFB=90°，
∴∠BAF=∠ABF=45°，
∴
，
同理：△BCG是等腰直角三角形，
，
∴
，
∴
；
②如图，OF∥BC，延长OF交AB于点I，
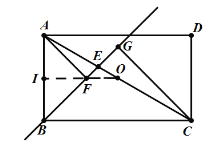
由①可知，△ABF是等腰直角三角形，
，
△BCG是等腰直角三角形，
，
∴
；
综合上述，FG的长度为：或.
故答案为：或.
