Question

【题目】如图所示，甲、乙两人在玩转盘游戏时，分别把转盘A，B分成3等份和1等份，并在每一份内标上数字．游戏规则：同时转动两个转盘，当转盘停止后，指针所在区域的数字之积为奇数时，甲获胜；当数字之积为偶数时，乙获胜．如果指针恰好在分割线上时，则需重新转动转盘．

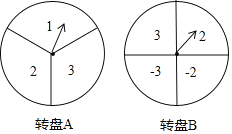
（1）利用画树状图或列表的方法，求甲获胜的概率．

（2）这个游戏规则对甲、乙双方公平吗？若公平，请说明理由；若不公平，请你在转盘A上只修改一个数字使游戏公平（不需要说明理由）．

Answer 1

【答案】（1）见解析，甲获胜概率为；（2）这个游戏规则对甲、乙双方不公平，将转盘A上的数字2改为1，则游戏公平．

【解析】

（1）列表得出所有等可能结果，从中找到符合条件的结果数，再根据概率公式计算可得；

（2）先计算出数字之积为偶数的概率，判断概率是否相等即可得知游戏是否公平．

解：（1）列表如下：

	﹣2	﹣3	2	3
1	﹣2	﹣3	2	3
2	﹣4	﹣6	4	6
3	﹣6	﹣9	6	9

由表可知，共有12种等可能结果，其中指针所在区域的数字之积为奇数的有4种结果，

所以甲获胜概率为；

（2）∵指针所在区域的数字之积为偶数的概率为，

∴这个游戏规则对甲、乙双方不公平，

将转盘A上的数字2改为1，则游戏公平．