题目内容
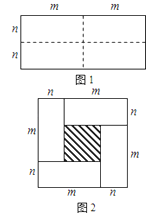
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请写出图2中阴影部分的面积;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2, (m﹣n)2, mn;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值.
【答案】(1)(m﹣n)2或(m+n)2﹣4mn;(2)(m﹣n)2=(m+n)2﹣4mn;(3)29
【解析】试题分析:(1)方法一:求出正方形的边长,再根据正方形面积公式求出即可;方法二:根据大正方形面积减去4个矩形面积,即可得出答案;(2)根据两种表示阴影部分的面积的方法,即可得出等式;(3)根据等式(a-b)2=(a+b)2-4ab即可解决.
试题解析:
(1)(m﹣n)2或(m+n)2﹣4mn;
(2)(m﹣n)2=(m+n)2﹣4mn;
(3)当a+b=7,ab=5时,
(a﹣b)2
=(a+b)2﹣4ab
=72﹣4×5
=49﹣20
=29.

练习册系列答案
相关题目
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
