Question

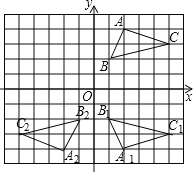
【题目】如图，在平面直角坐标系中，⊿ABC的三个顶点都在格点上，

(1)画出⊿ABC关于x轴对称的⊿A1B1C1.

(2)画出⊿ABC绕原点O旋转180°后的⊿A2B2C2，并写出A2、B2、C2的坐标

(3)假设每个正方形网格的边长为1，求⊿A1B1C1.的面积。

Answer 1

【答案】（1）作图见解析；（2）作图见解析；A2、B2、C2的坐标分别为（-2，-4），（-1，-2），（5，4）；（3）△A1B1C1的面积为．

【解析】试题分析：（1）先利用关于x轴对称的点的坐标特征写出A1、B1、C1的坐标，然后描点即可得到△A1B1C1；

（2）先利用关于原点对称的点的坐标特征写出A2、B2、C2的坐标，然后描点即可得到△A2B2C2；

（3）利用矩形的面积分别减去三个三角形的面积．

试题解析：（1）如图，△A1B1C1为所作；

（2）如图，△A2B2C2为所作，A2、B2、C2的坐标分别为（-2，-4），（-1，-2），（5，4）；

（3）△A1B1C1的面积=2×4-×2×1-×1×3-×4×1=．