题目内容

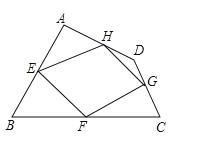
【题目】如图所示，AB∥CD，AD∥BC，OE＝OF，则图中全等三角形的组数是（ ）

A.3组B.4组C.5组D.6组

【答案】D

【解析】

先根据题意AB∥CD，AD∥BC，可得多对角相等，再利用平行四边形的性质可得线段相等，所以有△AFO≌△CEO，△AOD≌△COB，△FOD≌△EOB，△ACB≌△ACD，△ABD≌△DCB，△AOB≌△COD共6对．

∵AB∥CD，AD∥BC

∴∠ABD＝∠CDB，∠ADB＝∠CDB

又∵BD＝DB

∴△ABD≌△CDB

∴AB＝CD，AD＝BC

∵OA＝OC，OB＝OD

∴△ABO≌△CDO，△BOC≌△DOA

∵OB＝OD，∠CBD＝∠ADB，∠BOF＝∠DOE

∴△BFO≌△DEO

∴OE＝OF

∵OA＝OC，∠COF＝∠AOE

∴△COF≌△AOE

∵AB＝DC，BC＝AD，AC＝AC

∴△ABC≌△DCA，

共6组；

故选：D．

练习册系列答案
相关题目

【题目】如图，已知线段， 于点，且， 是射线上一动点， 、分别是， 的中点，过点， ， 的圆与的另一交点（点在线段上），连结， ．

（）当时，则的度数为__________．

（）在点的运动过程中，当时，取四边形一边的两端点和线段上一点，若以这三点为顶点的三角形是直角三角形，当时，则的值为__________．

【题目】如图，已知直线PA交⊙O于A、B两点，CD是⊙O的切线，切点且C，过点C作CD⊥PA于D，若AD：DC=1：3，AB=8，求⊙O的半径．

【题目】在平面直角坐标系中，已知A（3，0），以OA为一边在第一象限内画正方形OABC，D（m，0）为x轴上的一个动点，以BD为一边画正方形BDEF（点F在直线AB右侧）．

（1）当m＞3时（如图1），试判断线段AF与CD的数量关系，并说明理由．

（2）当AF=5时，求点E的坐标；

（3）当D点从A点向右移动4个单位，求这一过程中F点移动的路程是多少？

【题目】四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．

（1）四边形EFGH的形状是什么，并证明你的结论．

（2）当四边形ABCD的对角线满足什么条件时，四边形EFGH是矩形；并利用你给的条件加以证明．

【题目】如图，抛物线 与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴为=–1，P为抛物线上第二象限的一个动点．

（1）求抛物线的解析式并写出其顶点坐标；

（2）当点P的纵坐标为2时，求点P的横坐标；

（3）当点P在运动过程中，求四边形PABC面积最大时的值及此时点P的坐标．

【题目】某省计划5年内全部地级市通高铁.某高铁在泰州境内的建设即将展开，现有大量的沙石需要运输.某车队有载质量为8t、10t的卡车共12辆，全部车辆运输一次能运输100t沙石.

（1）求某车队载质量为8t、10t的卡车各有多少辆；

（2）随着工程的进展，某车队需要一次运输沙石165t以上,为了完成任务，准备新增购这两种卡车共7辆，车队有多少种购买方案?请你一一求出.

【题目】已知四边形ABCD是正方形，点P在直线BC上，点G在直线AD上（P，G不与正方形顶点重合，且在CD的同侧），PD=PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连结EF．

（1）如图1，当点P与点G分别在线段BC与线段AD上时．

①请直接写出线段DG与PC的数量关系(不要求证明）；

②求证：四边形PEFD是菱形；

（2）如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．

【题目】某公司有A、B两种型号的客车，它们的载客量、每天的租金如表所示：

A型号客车

B型号客车

载客量(人/辆)

45

30

租金(元/辆)

600

450

已知某中学计划租用A、B两种型号的客车共10辆，同时送七年级师生到沙家参加社会实践活动，已知该中学租车的总费用不超过5600元．

(1)求最多能租用多少辆A型号客车？

(2)若七年级的师生共有380人，请写出所有可能的租车方案．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网