题目内容
【题目】四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
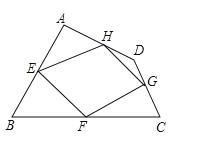
(1)四边形EFGH的形状是什么,并证明你的结论.
(2)当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形;并利用你给的条件加以证明.
【答案】(1)平行四边形;(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.
【解析】
(1)连接AC和BD,根据中位线知识得EH∥FG,EF∥HG,从而证明四边形EFGH为平行四边形;
(2)当AC⊥BD时,可证EH⊥HG,从而证明四边形EFGH为矩形.
解:(1)连接AC,BD,
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,FG∥BD,HG∥AC,EF∥AC,
∴EH∥FG,,EF∥HG,
∴四边形EFGH是平行四边形;
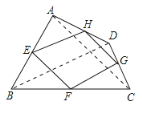
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形,理由如下:
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,FG∥BD,HG∥AC,EF∥AC,
∴EH∥FG,,EF∥HG,
∴四边形EFGH是平行四边形,
∵AC⊥BD,
∴EH⊥HG,
∴平行四边形EFGH是矩形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目