题目内容
【题目】如图,ΔABC中,AB=AC,将A沿DE折叠,使A与B重合,DE为折痕,若ΔBEC为等腰三角形,则∠A的度数是_________.

【答案】36或![]() .
.
【解析】
根据题意可知∠EBC≠∠C,所以若△BEC为等腰三角形,只能∠C=∠2或∠EBC=∠2;然后针对这两种情况,利用等腰三角形的性质、三角形的外角性质定理和三角形的内角和定理,设未知数列出方程,解方程即可得出结果.
解:如图1,根据题意,∠A=∠1,∵AB=AC,∴∠ABC=∠C,所以∠EBC≠∠C,
若△BEC为等腰三角形,只能∠C=∠2或∠EBC=∠2;
当∠C=∠2时,设∠A=x,则∠2=∠A+∠1=2x,∴∠C=2x=∠ABC,
在△ABC中,∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°,
解得:x=36°,即∠A=36°;

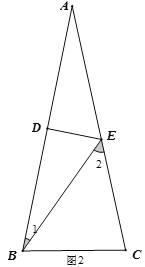
当∠EBC=∠2时,如图2,设∠A=y,则∠2=∠A+∠1=2y,∴∠EBC=2y,
∴∠ABC=3y=∠C,
在△ABC中,∵∠A+∠ABC+∠C=180°,∴y+3y+3y=180°,
解得:![]() ,即∠A=
,即∠A=![]() .
.
综上,∠A的度数是:36或![]() .
.
故答案为:36或![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目




