题目内容
【题目】如图,在四边形ABCD中,对角线AC、BD交于点F,AC⊥AB于点A,点E在边CD上,且满足DFDB=DEDC,FE=FB,BD平分∠ABE,若AB=6,CF=9,则OE的长为_____.
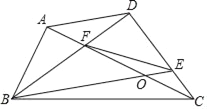
【答案】2
【解析】分析:首先证明△BAF∽△CAB,推出AB2=AFAC,设AF=x,则有36=x(x+9),解得x=3,推出AF=3,BF=EF=![]() =3
=3![]() ,BC=
,BC=![]() =6
=6![]() ,由△EOF∽△COB,推出
,由△EOF∽△COB,推出![]() =
=![]() =
=![]() =
=![]() ,设OF=a,OB=2a,在Rt△ABO中,根据AB2+AO2=OB2,可得36+(3+a)2=4a2,求出a即可解决问题.
,设OF=a,OB=2a,在Rt△ABO中,根据AB2+AO2=OB2,可得36+(3+a)2=4a2,求出a即可解决问题.
详解:如图:
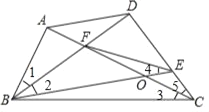
∵DFDB=DEDC,
∴![]() =
=![]() ,
,
∵∠EDF=∠BDC,
∴△CDF∽△BDE,
∴∠2=∠5,
∵∠FOB=∠EOC,
∴△BOF∽△COE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴△EOF∽△COB,
∴∠3=∠4,
∵FB=FE,
∴∠2=∠4,
∵∠1=∠2,
∴∠1=∠2=∠3,∵∠BAF=∠CAB,
∴△BAF∽△CAB,
∴AB2=AFAC,
设AF=x,则有36=x(x+9),解得x=3,
∴AF=3,BF=EF=![]() =3
=3![]() ,
,
BC=![]() =6
=6![]() ,
,
∵△EOF∽△COB,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
设OF=a,OB=2a,
在Rt△ABO中,∵AB2+AO2=OB2,
∴36+(3+a)2=4a2,
解得a=5,
∴OF=5,OC=4,
∴OE=2.
故答案为2.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | 0.35 |
一般 | m | |
不好 | 36 |
请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了 名学生;
(2)m= ;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.