Question

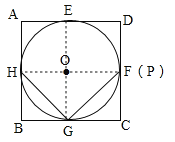
【题目】如图，边长为4的正方形ABCD外切于⊙O，切点分别为E、F、G、H．则图中阴影部分的面积为______．

Answer 1

【答案】2π+4．

【解析】解：如图，连接HO，延长HO交CD于点P，∵正方形ABCD外切于⊙O，∴∠A=∠D=∠AHP=90°，∴四边形AHPD为矩形，∴∠OPD=90°，又∠OFD=90°，∴点P于点F重合，则HF为⊙O的直径，同理EG为⊙O的直径，由∠B=∠OGB=∠OHB=90°且OH=OG知，四边形BGOH为正方形，同理四边形OGCF、四边形OFDE、四边形OEAH均为正方形，∴BH=BG=GC=CF=2，∠HGO=∠FGO=45°，∴∠HGF=90°，GH=GF= =，则阴影部分面积=S⊙O+S△HGF=π22+××=2π+4．故答案为：2π+4．