Question

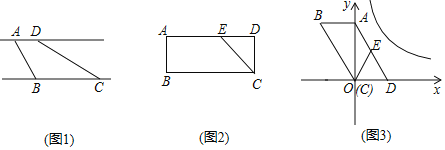
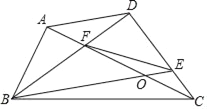
【题目】如图1，在正方形中，点，分别是边，上的点，且.连接，过点作，使，连接，.

（1）请判断：与的数量关系是________________，位置关系是___________________；

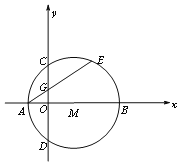
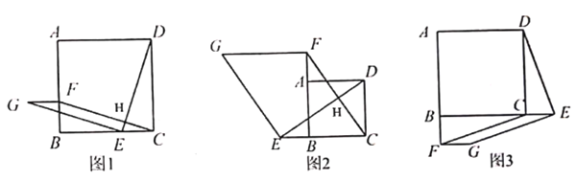
（2）如图2，若点，分别是边，延长线上的点，其它条件不变，（1）中结论是否仍然成立？请作出判断并给予证明；

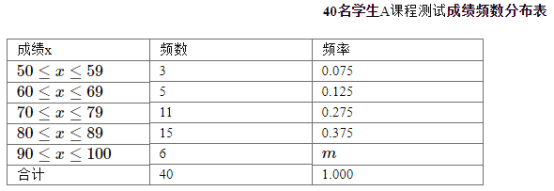
（3）如图3，若点，分别是边，延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断.

Answer 1

【答案】（1）；．（2）成立；（3）成立．

【解析】

（1）构造辅助线后证明△HGE≌△CED，利用对应边相等求证四边形GHBF是矩形后，利用等量代换即可求出FG=CE，FG∥CE；
（2）构造辅助线后证明△HGE≌△CED，利用对应边相等求证四边形GHBF是矩形后，利用等量代换即可求出FG=CE，FG∥CE；
（3）证明△CBF≌△DCE，即可证明四边形CEGF是平行四边形，即可得出结论．

解：（1）FG=CE，FG∥CE；理由如下：
过点G作GH⊥CB的延长线于点H，如图1所示：

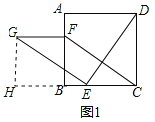
则GH∥BF，∠GHE=90°，
∵EG⊥DE，
∴∠GEH+∠DEC=90°，
∵∠GEH+∠HGE=90°，
∴∠DEC=∠HGE，
在△HGE与△CED中，

∴△HGE≌△CED（AAS），
∴GH=CE，HE=CD，
∵CE=BF，
∴GH=BF，
∵GH∥BF，
∴四边形GHBF是矩形，
∴GF=BH，FG∥CH
∴FG∥CE，
∵四边形ABCD是正方形，
∴CD=BC，
∴HE=BC，
∴HE+EB=BC+EB，
∴BH=EC，
∴FG=EC；
故答案为：FG=CE，FG∥CE；

（2）FG=CE，FG∥CE仍然成立；理由如下：
过点G作GH⊥CB的延长线于点H，如图2所示：

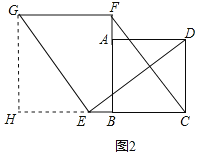
∵EG⊥DE，
∴∠GEH+∠DEC=90°，
∵∠GEH+∠HGE=90°，
∴∠DEC=∠HGE，
在△HGE与△CED中，

∴△HGE≌△CED（AAS），
∴GH=CE，HE=CD，
∵CE=BF，∴GH=BF，
∵GH∥BF，
∴四边形GHBF是矩形，
∴GF=BH，FG∥CH
∴FG∥CE，
∵四边形ABCD是正方形，
∴CD=BC，
∴HE=BC，
∴HE+EB=BC+EB，
∴BH=EC，
∴FG=EC；

（3）FG=CE，FG∥CE仍然成立．理由如下：
∵四边形ABCD是正方形，
∴BC=CD，∠FBC=∠ECD=90°，
在△CBF与△DCE中，

∴△CBF≌△DCE（SAS），
∴∠BCF=∠CDE，CF=DE，
∵EG=DE，∴CF=EG，
∵DE⊥EG
∴∠DEC+∠CEG=90°
∵∠CDE+∠DEC=90°
∴∠CDE=∠CEG，
∴∠BCF=∠CEG，
∴CF∥EG，
∴四边形CEGF平行四边形，
∴FG∥CE，FG=CE．