题目内容
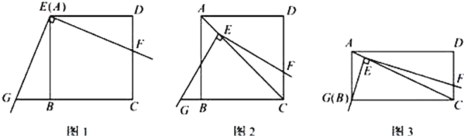
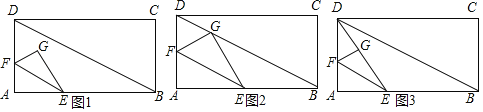
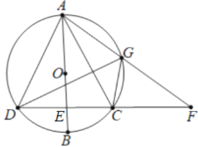
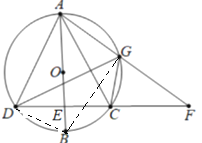
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E ,G是弧AC上的点,AG,DC延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)若BE=2,CD=8,求AD的长.
【答案】(1)详见解析;(2)AD=4![]() .
.
【解析】
(1) 连接GB,根据直径所对的圆周角是直角得到![]() 和
和![]() ,再证明
,再证明![]() ,用等量替换即可证明
,用等量替换即可证明![]() ;
;
(2) 连接DB,DO,先用勾股定理求出BD的长度,再用勾股定理计算圆的半径,再用一次勾股定理即可得到答案;
解:(1)如图,连接GB,
 ,
,
∵AB是直径,
∴![]() (直径所对的圆周角是直角),
(直径所对的圆周角是直角),
∴![]() ,
,
又∵AB是⊙O的直径,弦CD⊥AB于点E ,
∴AB垂直平分DC,
∴弧DB=弧BC,
∴![]() (同弧所对的圆周角相等),
(同弧所对的圆周角相等),
又![]() ,
,
![]() ,
,
由![]() 得到
得到![]() (等量替换);
(等量替换);
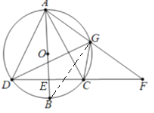
(2)如图,连接DB,DO,
∵AB是⊙O的直径,弦CD⊥AB于点E ,
∴AB平分CD,即DE=CE,
∵CD=8,
∴DE=4,
根据勾股定理得到:![]() ,
,
∴![]() ,
,
设圆的半径为r,根据勾股定理得到:
![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
又在![]() 中,
中,
∵AB是直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
A公司方案:无纺布的价格均为每吨1.95万元![]() ;
;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
设甲厂在同一公司一次购买无纺布的数量为x吨(x>0).
(Ⅰ)根据题意,填写下表:
一次购买数量(吨) | 10 | 20 | 35 | … |
A公司花费(万元) | 39 | … | ||
B公司花费(万元) | 40 | … |
(Ⅱ) 设在A公司花费![]() 万元,在B公司花费
万元,在B公司花费![]() 万元,分别求
万元,分别求![]() 、
、![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)如果甲厂所需购买的无纺布是50吨,试通过计算说明选择哪家公司费用较少.