题目内容
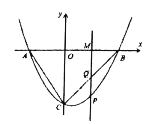
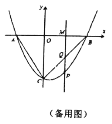
【题目】如图,一次函数![]() 的图象与抛物线
的图象与抛物线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,抛物线交
点,抛物线交![]() 轴的另一个交点为点
轴的另一个交点为点![]() (点
(点![]() 的左边).点
的左边).点![]() 为抛物线上一个动点(且点
为抛物线上一个动点(且点![]() 的横坐标
的横坐标![]() 满足
满足![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() .
.
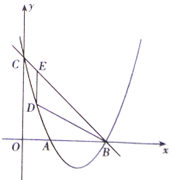
(1)求该抛物线的解析式;
(2)若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标;
的坐标;
(3)在(2)的结论下,点![]() 为抛物线上任意一个动点,点
为抛物线上任意一个动点,点![]() 为
为![]() 轴上一个动点,则以
轴上一个动点,则以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形能否为平行四边形,若能,请直接写出点
四点为顶点的四边形能否为平行四边形,若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)y=x2﹣4x+3;(2)D点坐标为D1(1,0),D2(2,﹣1);(3)能,![]() ,
,![]()
【解析】
(1)先求出点B、C的坐标,然后利用待定系数法,即可求出抛物线的解析式;
(2)根据题意,可分为两种情况进行①当点D1为直角顶点时,点D1与点A重合;②当点B为△BD2E2的直角顶点时;分别求出坐标即可;
(3)由题意,利用平行四边形的判定和性质,通过平移直线BD进行讨论,即可求出点P的坐标.
解:(1)由一次函数![]() 的图象交x轴于B点,交y轴于C点可得,
的图象交x轴于B点,交y轴于C点可得,
∴B(3,0),C(0,3),
把B、C代入抛物线![]() 可得,
可得,
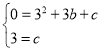 ,
,
∴![]()
∴抛物线为y=x2﹣4x+3;
(2)分两种情况:
①当点D1为直角顶点时,点D1与点A重合;
令y=0,得x2﹣4x+3=0,
解得:x1=1,x2=3;
∵点B在点A的右边,
∴A(1,0),B(3,0);
∴D1(1,0);
②当点B为△BD2E2的直角顶点时;
∵OB=OC,∠BOC=90°,
∴∠OBE2=45°;
当∠E2BD2=90°时,∠OBD2=45°,
∴BO平分∠E2BD2;
又∵D2E2∥y轴,
∴D2E2⊥BO,
∴D2、E2关于x轴对称;
直线BC的函数关系式为y=﹣x+3;
设E2(x,﹣x+3),D2(x,x2﹣4x+3),
则有:(﹣x+3)+(x2﹣4x+3)=0,
即x2﹣5x+6=0;
解得:x1=2,x2=3(舍去);
∴当x=2时,y=x2﹣4x+3=22﹣4×2+3=﹣1;
∴D2的坐标为D2(2,﹣1).
∴D点坐标为D1(1,0),D2(2,﹣1);
(3)由(2)知,当D点的坐标为D1(1,0)时,不能构成平行四边形;
当点D的坐标为D2(2,﹣1)(即抛物线顶点)时,
平移直线BD交x轴于点N,交抛物线于P;
∵D(2,﹣1),
∴可设P(x,1);
∴x2﹣4x+3=1,
解得:![]() ,
,![]() ;
;
∴符合条件的P点有两个,
即![]() ,
,![]() .
.

【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
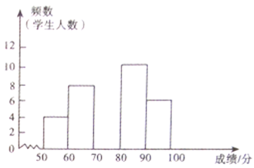
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?