题目内容
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时= ![]() 米/秒)
米/秒) 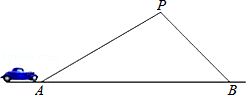
【答案】解:过点P作PC⊥AB于点C. 在Rt△APC中,tan∠PAC= ![]() ,
,
∴AC= ![]() =50
=50 ![]() ≈86.5(米),
≈86.5(米),
同理,BC= ![]() =PC=50(米),
=PC=50(米),
∴AB=AC+BC≈136.5(米),
60千米/时= ![]() 米/秒,
米/秒,
则136.5÷ ![]() ≈8.2>8.1.
≈8.2>8.1.
故这辆车通过AB段超速.
【解析】过点P作PC⊥AB于点C,在Rt△APC中,tan∠PAC= ![]() ,代入数据可得AC的长,同理可得BC的长,然后再求和即可得到AB的长,再利用路程初一速度可得时间,再与8.1秒进行比较,可得答案.
,代入数据可得AC的长,同理可得BC的长,然后再求和即可得到AB的长,再利用路程初一速度可得时间,再与8.1秒进行比较,可得答案.

练习册系列答案
相关题目
【题目】甲、乙两人参加操作技能培训,他们在培训期间参加的5次测试成绩(满分10分)记录如下:
5次测试成绩(分) | 平均数 | 方差 | |||||
甲 | 8 | 8 | 7 | 8 | 9 | 8 | 0.4 |
乙 | 5 | 9 | 7 | 10 | 9 | 8 | 3.2 |
(1)若从甲、乙两人中选派一人参加操作技能大赛,你认为应选谁?为什么?
(2)如果乙再测试一次,成绩为8分,请计算乙6次测试成绩的方差(结果保留小数点后两位).