题目内容
【题目】如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
(1)过点F作FH⊥BE于点H,证明: ![]() =
= ![]() ;
;
(2)猜想:BE、AE、EF之间的数量关系,并证明你的结论;
(3)若DG=2,求AE值.
【答案】
(1)
证明:∵在正方形ABCD中,AD∥BC,
∴∠AEB=∠EBF,
又∵FH⊥BE,
∴∠A=∠BHF=90°,
∴△ABE∽△HFB,
∴ ![]() =
= ![]()
(2)
BE2=2AEEF,
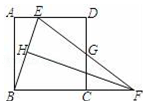
证明如下:∵∠FBE=∠FEB,
∴BF=EF,
∵FH⊥BE,
∴FH是等腰△FBE底边上的中线,
∴BH= ![]() BE,
BE,
由(1)得, ![]() ,
,
∴ ![]()
∴BE2=2AEBF;
∵BF=EF,
∴BE2=2AEEF
(3)
解:∵DG═2,
∴正方形ABCD的边长为4,
设AE=k(0<k<4),
则DE═4﹣k,BF=8﹣k,
在Rt△ABM中,BE2=AB2+AE2=16+k2,
由BE2=2AEBF,得16+k2=2k(8﹣k),
即3k2﹣16k+16=0,解得 k= ![]() 或k=4
或k=4
∵k≠4,
∴AE= ![]()
【解析】(1)根据正方形的性质得到∠AEB=∠EBF,由已知条件得到∠A=∠BHF,根据相似三角形的判定定理即可得到结论;(2)根据已知条件得到FH是等腰△FBE底边上的高,求得BH= ![]() BE,由根据相似三角形的性质得到
BE,由根据相似三角形的性质得到 ![]() ,等量代换即可得到结论;(3)由已知条件得到正方形ABCD的边长为4,设AE=k(0<k<2),则DE═4﹣k,BF=8﹣k,根据勾股定理列方程即可得到结果.
,等量代换即可得到结论;(3)由已知条件得到正方形ABCD的边长为4,设AE=k(0<k<2),则DE═4﹣k,BF=8﹣k,根据勾股定理列方程即可得到结果.

练习册系列答案
相关题目