题目内容
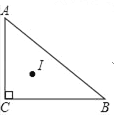
【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．
（1）在方格纸中作出与△ABC关于原点对称的△A1B1C1，并写出点A
、B、C的坐标；
（2）求出过A、B、O三点的抛物线的对称轴．
【答案】（1）作图见解析；（2）x=-3.
【解析】
试题（1）根据网格结构找出点A、B、C关于坐标原点O的对称点A1、B1、C1的位置，然后顺次连接即可，再根据平面直角坐标系写出各点的坐标即可；
（2）因为A1（﹣1，4），B1（﹣5，4），纵坐标相同，所以A
B∥x轴，所以过A、B、O三点的抛物线的对称轴是直线x=
=
．
试题解析：（1）△A1B1C1如图所示，A1（﹣1，4），B1（﹣5，4），C1（﹣4，1）；
（2）过A、B、O三点的抛物线的对称轴是直线x==．
【题目】西安市某中学九年级组织了一次数学计算比赛（禁用计算器），每班选25名同学参加比赛，成绩分为A，B，C，D四个等级，其中A等级得分为100分，B等级得分为85分，C等级得分为75分，D等级得分为60分，数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图，请根据提供的信息解答下列问题．
（1）把一班竞赛成绩统计图补充完整．
（2）填表：
平均数（分） | 中位数（分） | 众数（分） | |
一班 |
|
| 85 |
二班 | 84 | 75 |
|
（3）请从以下给出的两个方面对这次比赛成绩的结果进行①从平均数、众数方面来比较一班和二班的成绩；②从B级以上（包括B级）的人数方面来比较一班和二班的成绩．
【题目】某玩具厂工人的工作时间：每月25天，每天8小时．待遇：按件计酬．多劳多得，每月另加福利工资100元，按月结算．该厂生产A，B两种产品，工人每生产一件A产品，可得报酬
元，每生产一件B产品，可得报酬
元．下表记录的是工人小李的工作情况：
生产A产品的数量 | 生产B声品的数量 | 总时间 |
1 | 1 | 35 |
3 | 2 | 85 |
根据上表提供的信息，请回答下列问题：
小李每生产一件A产品、每生产一件B产品，分别需要多少分钟？
设小李某月生产A产品x件，该月工资为y元，求y与x的函数表达式．
如果生产各种产品的数目没有限制，那么小李该月的工资最多为多少？
