题目内容
【题目】已知A,B,C,D是⊙O上的四个点.
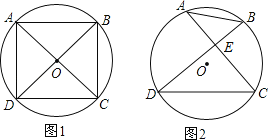
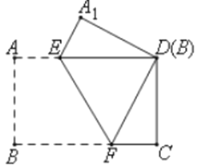
(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
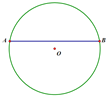
(2)如图2,若AC⊥BD.垂足为E,AB=4,DC=6,求⊙O的半径.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据题意不难证明四边形ABCD是正方形,从而得证;
(2)连接DO,延长交圆O于F,连接CF、BF.根据直径所对的圆周角是直角,得∠DCF=∠DBF=90°,则BF∥AC,根据平行弦所夹的弧相等,得![]() ,则CF=AB.根据勾股定理即可求解.
,则CF=AB.根据勾股定理即可求解.
(1)∵∠ADC=∠BCD=90°,
∴AC、BD是⊙O的直径,
∴∠DAB=∠ABC=90°,
∴四边形ABCD是矩形,
∵AD=CD,
∴四边形ABCD是正方形,
∴AC⊥BD;
(2)连接DO,延长交圆O于F,连接CF、BF.
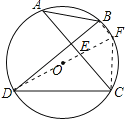
∵DF是直径,
∴∠DCF=∠DBF=90°,
∴FB⊥DB,
又∵AC⊥BD,
∴BF∥AC,∠BDC+∠ACD=90°,
∵∠FCA+∠ACD=90°,
∴∠BDC=∠FCA=∠BAC,
∴四边形ACFB是等腰梯形,
∴CF=AB.
根据勾股定理,得CF2+DC2=AB2+DC2=DF2=52,
∴DF=2![]() ,
,
∴OD=![]() ,即⊙O的半径为
,即⊙O的半径为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标x纵坐标y的对应值如下表
上部分点的横坐标x纵坐标y的对应值如下表
x |
|
|
| 0 | 1 | 2 |
|
y |
| 0 |
|
| 0 | 8 |
|
![]() 写出该抛物线的对称轴及当
写出该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
![]() 求出抛物线
求出抛物线![]() 的解析式,并在平面直角坐标系中画出该抛物线的图象;
的解析式,并在平面直角坐标系中画出该抛物线的图象;
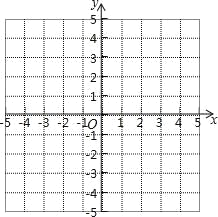
(3)结合图象回答:
①不等式![]() 的解集是___________________;
的解集是___________________;
②当![]() 时,y的取值范围是__________________.
时,y的取值范围是__________________.