题目内容
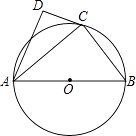
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.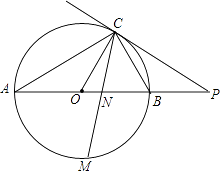
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MNMC的值.
【答案】
(1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB
AB
(3)解:连接MA,MB,
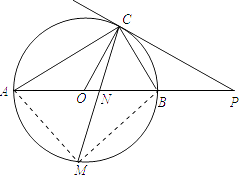
∵点M是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ![]() =
= ![]() .
.
∴BM2=MNMC.
又∵AB是⊙O的直径, ![]() =
= ![]() ,
,
∴∠AMB=90°,AM=BM.
∵AB=8,
∴BM=4 ![]() .
.
∴MNMC=BM2=32.
【解析】(1)利用直径上的圆周角是直角和圆的定义易证;
(2)利用等腰三角形的性质和直角三角形的性质来证明;
(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,从而可证得△MBN∽△MCB.再利用相似三角形的对应边成比例得到BM2=MNMC.在Rt△ABM中求出BM,即可得到结论.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案