题目内容
【题目】如图，B位于A南偏西37°方向， 港口C位于A南偏东35°方向，B位于C正西方向． 轮船甲从A出发沿正南方向行驶40海里到达点D处，此时轮船乙从B出发沿正东方向行驶20海里至E处，E位于D南偏西45°方向．这时，E处距离港口C有多远？ （参考数据：tan37°≈0.75，tan35°≈0.70）
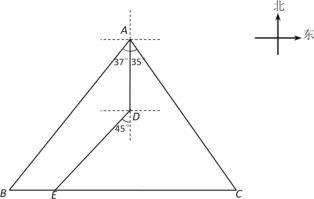
【答案】E处距离港口C约96海里
【解析】
延长AD交BC于点F，设EF＝x海里，得DF＝x海里，解Rt△ABF得EF=40海里，AF=80海里，再解Rt△AFC得CF=56海里，从而可得EC=96海里．
如图，延长AD交BC于点F，AF⊥BC ．
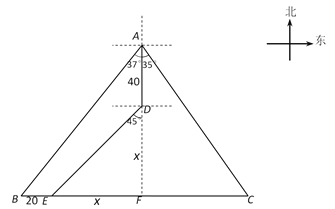
设EF＝x海里．
在Rt△DEF中，∠DFE＝90°，
∵tan∠EDF＝
，
∴tan45°＝
，
∴ DF＝x，
在Rt△ABF中，∠DFE＝90°，
∵tan∠BAF＝
，
∴BF＝AF tan37°，
∴20＋x≈0．75(40＋x)，
∴x＝40，
∴AF＝AD＋DF＝80．
在Rt△AFC中，∠AFC＝90°，
∵tan∠CAF＝
，
∵tan35°＝，
∴CF＝AFtan35°≈80×0．70＝56
∴CE＝EF＋CF＝40＋56＝96
答：E处距离港口C约96海里．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：
售价x（元/千克） | 50 | 60 | 70 |
销售量y（千克） | 100 | 80 | 60 |
（1）求y与x之间的函数表达式；
（2）设商品每天的总利润为W（元），求W与x之间的函数表达式（利润＝收入﹣成本）；并求出售价为多少元时获得最大利润，最大利润是多少？
