题目内容
【题目】四边形ABCD的对角线AC、BD的长分别为10厘米、6厘米,且AC与BD互相垂直,顺次连接四边形ABCD四边的中点E、F、G、H得四边形EFGH,则四边形EFGH的面积为_____平方厘米.
【答案】15
【解析】
利用三角形中位线定理可证明四边形EFGH是矩形,然后求出矩形的两邻边长即可求出面积.
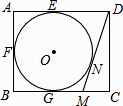
解:如图所示:

在△ABC中,E、F分别是AB、BC的中点,
∴EF=![]() AC=5厘米,EF∥AC,
AC=5厘米,EF∥AC,
在△ADC中,H、G分别是AD、CD的中点,
∴HG=![]() AC=5厘米,HG∥AC,
AC=5厘米,HG∥AC,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形,
在△ABD中,E、H分别是AB、AD的中点,
∴EH=![]() BD=3厘米,EH∥BD,
BD=3厘米,EH∥BD,
∵AC⊥BD,
∴EF⊥EH,
∴四边形EFGH是矩形,
∴四边形EFGH的面积为:5×3=15平方厘米.
故答案为:15.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?