Question

【题目】在△ABC中, AB=BC,O是AC的中点，P是AC上的一个动点（P点不与点A,O,C重合）．过点A,点C作直线BP的垂线，垂足分别为点E和点F，连接OE,OF．

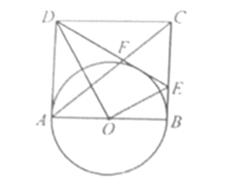
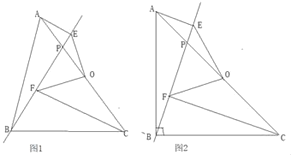
（1）如图1，判断线段OE与OF的数量关系是什么，请说明理由；

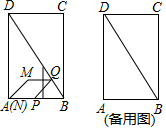
（2）如图2，当∠ABC=90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由?

Answer 1

【答案】（1）OF=OE，理由见解析；（2）OF⊥OE，OF=OE．理由见解析；

【解析】

（1）如图1中，延长EO交CF于K．首先证明△AOE≌△COK，推出OE=OK即可解决问题；
（2）如图2中，延长EO交CF于K．由△ABE≌△BCF，推出BE=CF，AE=BF，由△AOE≌△COK，推出AE=CK，OE=OK，推出FK=EF，可得△EFK是等腰直角三角形，即可解决问题；

解：（1）如图1中，延长EO交CF于K．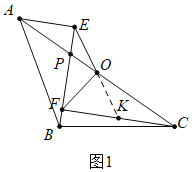

∵AE⊥BE，CF⊥BE，
∴AE∥CK，
∴∠EAO=∠KCO，
∵OA=OC，∠AOE=∠COK，
∴△AOE≌△COK（ASA），
∴OE=OK，
∵△EFK是直角三角形，
∴OF=EK=OE．
（2）如图2中，延长EO交CF于K．

∵∠ABC=∠AEB=∠CFB=90°，
∴∠ABE+∠BAE=90°，∠ABE+∠CBF=90°，
∴∠BAE=∠CBF，
∵AB=BC，
∴△ABE≌△BCF，
∴BE=CF，AE=BF，
∵△AOE≌△COK，
∴AE=CK，OE=OK，
∴FK=EF，
∴△EFK是等腰直角三角形，
∴OF⊥EK，OF=OE．