Question

【题目】已知抛物线(b，c为常数)．

（1）若抛物线的顶点坐标为(1，1)，求b，c的值；

（2）若抛物线上始终存在不重合的两点关于原点对称，求c的取值范围；

（3）在（1）的条件下，存在正实数m，n( m＜n)，当m≤x≤n时，恰好有，求m，n的值．

Answer 1

【答案】（1）b=6，c=2019；（2） ；（3）m=1，

【解析】

（1）利用抛物线的顶点坐标和二次函数解析式y=-2x2+（b-2）x+（c-2020）可知，y=-2（x-1）2+1，易得b、c的值；

（2）设抛物线线上关于原点对称且不重合的两点坐标分别是（x0，y0），（-x0，-y0），代入函数解析式，经过化简得到c=2x02+2020，易得c>2020；

（3）由题意知，抛物线为y=-2x2+4x-1=-2（x-1）2+1，则y≤1．利用不等式的性质推知：≤y≤，易得1≤m＜n．由二次函数图象的性质得到：当x=m时，y最大值=-2m2+4m-1．当x=n时，y最小值=-2n2+4n-1．所以=-2m2+4m-1，=-2n2+4n-1通过解方程求得m、n的值．

（1）由题可设

去括号得：y=－2x2+4x－1

，

b=6，c=2019

（2）设抛物线上关于原点对称且不重合的两点坐标分别为、

代入解析式可得：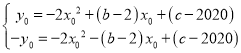

两式相加可得：－4x02+2（c－2020）=0

c=2x02+2020

∵x≠0，

，

（3）由（1）可知抛物线为y=－2x2+4x－1=－2（x－1）2+1，

∴y≤1，

∵0＜m＜n，当m≤x≤n时，恰好有，

，

，即m≥1，

∴1≤m＜n，

∵抛物线对称轴x=1，开口向下，

∴当m≤x≤n时，y随x增大而减小，

∴当x=m时，ymax=－2m2+4m－1，

当x=n时，ymin=－2n2+4n－1，

又，

，

将①整理得：2n3－4n2+n+1=0

∴变形得：（2n3－2n2）－（2n2－n－1）=0

即：2n2（n－1）－（2n+1）（n－1）=0

∴（n－1）（2n2－2n－1）=0

∵n＞1

∴2n2－2n－1=0

（舍去），

同理整理②得：（m－1）（2m2－2m－1）=0

∵1≤m＜n

∴m1=1，（舍去），（舍去）

∴综上所示：m=1，