题目内容
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.
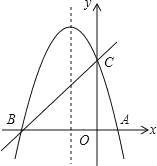
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴上的一个动点,求使△BPC为直角三角形的点P的坐标.
【答案】(1)y=-x2-2x+3;(2)(-1,2);(3)(-1,-2)或(-1,4)或(-1,![]() )或(-1,
)或(-1,![]() ).
).
【解析】
试题分析:(1)先把点B代入y=x+m,求得m的值,求得C的坐标,然后根据待定系数法即可求得抛物线的解析式;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值,即可求出点P的坐标.
试题解析:(1)把B(-3,0)代入y=x+m,
得-3+m=0,m=3,
∴直线的解析式为y=x+3;
∴点C的坐标为(0,3),
∵OC=3OA,
∴点A的坐标为(1,0),
∴ ,解得
,解得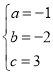 ,
,
∴抛物线的解析式为y=-x2-2x+3;
(2)∵y=-x2-2x+3=-(x+1)2+4,
∴对称轴是直线x=-1,
设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得,y=2,
∴M(-1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2);
(3)设P(-1,t),又∵B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,
①若点B为直角顶点,则BC2+PB2=PC2
即:18+4+t2=t2-6t+10解之得:t=-2;
②若点C为直角顶点,则BC2+PC2=PB2
即:18+t2-6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2
即:4+t2+t2-6t+10=18解之得:t1=![]() ,t2=
,t2=![]() ;
;
综上所述P的坐标为(-1,-2)或(-1,4)或(-1,![]() )或(-1,
)或(-1,![]() ).
).

