题目内容
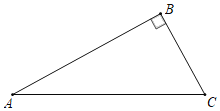
【题目】如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= °;若∠MON=90°,则∠ACG= °;
(2)若∠MON=n°,请求出∠ACG的度数;(用含n的代数式表示)
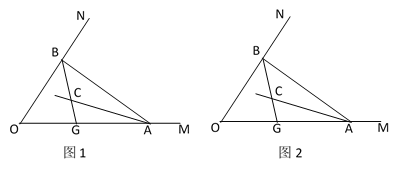
(3)如图2,若∠MON=n°,过C作直线与AB交于F,若CF∥OA时,求∠BGO-∠ACF的度数.(用含n的代数式表示).
【答案】(1)60°;45°;(2)90°-![]() n;(3)90°-
n;(3)90°-![]() n.
n.
【解析】
(1)根据三角形的内角和求出∠ABO+∠BAO的度数,再根据角平分线的定义及外角的性质即可得到∠ACG的度数;
(2)根据(1)中的结论即可求出答案;
(3)根据角平分线的性质,平行线的性质得到∠ACF=∠CAO=∠BAC,利用外角的性质得到∠BGO-∠ACF=∠ACG,由此得到答案.
(1)∵∠MON+∠ABO+∠BAO=180°,
∴∠ABO+∠BAO=180°-∠MON,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠ABC=![]() ∠ABO,∠BAC=
∠ABO,∠BAC=![]() ∠BAO,
∠BAO,
当∠MON=60°,
∠ACG=∠ABC+∠BAC=![]() (∠ABO+∠BAO)=
(∠ABO+∠BAO)=![]() (180°-∠MON)=60°,
(180°-∠MON)=60°,
当∠MON=90°,
∠ACG=∠ABC+∠BAC=![]() (∠ABO+∠BAO)=
(∠ABO+∠BAO)=![]() (180°-∠MON)=45°,
(180°-∠MON)=45°,
故答案为:60°,45°;
(2)由(1)知∠ACG=![]() (180°-∠MON),
(180°-∠MON),
∵∠MON=n°,
∴∠ACG=![]() (180°-∠MON)=90°-
(180°-∠MON)=90°-![]() n;
n;
(3)∵AC平分∠BAO,
∴∠BAC=∠CAO
∵CF∥OA,
∴∠ACF=∠CAO=∠BAC,
∵∠BGO=∠ABG+∠BAO=∠ABG+2∠ACF,
∴∠BGO-∠ACF=∠ABG+2∠ACF-∠ACF=∠ABG+∠ACF=∠ABG+∠BAC=∠ACG,
∵∠MON=n°时∠ACG=90°-![]() n,
n,
∴∠BGO-∠ACF=90°-![]() n.
n.

 阅读快车系列答案
阅读快车系列答案