题目内容

【题目】已知，如图，在直角三角形ABC中，∠ABC＝90°，AC＝10，BC＝6，AB＝8．P是线段AC上的一个动点，当点P从点C向点A运动时，运动到点A停止，设PC＝x，△ABP的面积为y．求y与x之间的关系式．

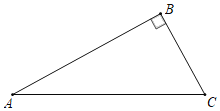
【答案】y＝﹣x+24．

【解析】

过点B作BD⊥AC于D，则BD为AC边上的高．根据△ABC的面积不变即可求出BD；根据三角形的面积公式得出S△ABP＝APBD，代入数值，即可求出y与x之间的关系式．

如图，过点B作BD⊥AC于D．

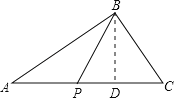
∵S△ABC＝ACBD＝ABBC，

∴BD＝；

∵AC＝10，PC＝x，

∴AP＝AC﹣PC＝10﹣x，

∴S△ABP＝APBD＝×（10﹣x）×＝﹣x+24，

∴y与x之间的关系式为：y＝﹣x+24．

练习册系列答案
相关题目

【题目】直线L与y＝2x+1的交于点A（2，a），与直线y＝x+2的交于点B（b，1）

（1）求a，b的值；

（2）求直线l的函数表达式；

（3）求直线L、x轴、直线y＝2x+1围成的图形的面积．

【题目】如图是本地区一种产品30天的销售图象，图1是产品日销售量y（单位：件）与时间t（单位：天）的函数关系，图2是一件产品的销售利润z（单位，元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列正确结论的序号是____．

①第24天的销售量为200件；

②第10天销售一件产品的利润是15元；

③第12天与第30天这两天的日销售利润相等；

④第30天的日销售利润是750元．

【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单，为了尽快交货，增开了一条生产线，实际每月生产能力比原计划提高了50%，结果比原计划提前5个月完成交货，求每月实际生产智能手机多少万部．

【题目】如图，以直线上一点为端点作射线，使，将一个直角三角形的直角顶点放在点处，（注，）

（1）如图①，若直角三角板的一边放在射线上，则______°；

（2）如图②，将直角三角板绕点逆时针方向转动到某个位置，若恰好平分，求的度数；

（3）如图③，将直角三角板绕点转动，如果始终在的内部，试猜想和有怎样的数量关系？并说明理由．

【题目】如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是__________

【题目】为提高学生的爱国意识，陶冶爱国情操，某中学举行了以“厉害了，我的国”为主题的书法绘画大赛，该校九年级共有三个班都参加了这次活动，三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示：

收集数据：

数据

（1）请填写下表：

得出结论：

（2）如果在每个班级参加决赛的选手中分别选出3人参加总决赛，你认为哪个班级的实力更强一些?请简要说明理由.

【题目】如图1，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．

（1）若∠MON＝60°，则∠ACG＝ °；若∠MON＝90°，则∠ACG＝ °；

（2）若∠MON＝n°，请求出∠ACG的度数；（用含n的代数式表示）

（3）如图2，若∠MON＝n°，过C作直线与AB交于F，若CF∥OA时，求∠BGO－∠ACF的度数．（用含n的代数式表示）．

【题目】在一次数学社团活动中，指导老师给同学们提出了以下问题：

问题：有67张卡片叠在一起，按从上而下的顺序先把第一张拿走，把第二张放到底层，然后把第三张拿走，再把第四张放到底层，如此进行下去，直至只剩最后一张卡片.问仅剩的这张卡片是原来的第几张卡片？

由于卡片数量较多，指导老师建议同学们先对较少的张数进行尝试，以便熟悉游戏规则并发现一些规律！

（1）请你试着在草稿纸上进行试验，将试验结果填写在下表中：

试验的卡片数量

（张）

2

4

8

9

10

11

剩下最后一张卡片是

原来卡片的第几张

（2）根据试验结果的规律，回答最初的67张卡片情形，请你给出答案并简要说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网