题目内容
如图,菱形ABCD中,对角线AC、BD交于点O,点P在对角线BD上运动(B、D两点除外),线段PA绕点P顺时针旋转m°(0<m°<180º) 得线段PQ.

(1)当点Q与点D重合,请在图中用尺规作出点P所处的位置(不写作法,保留作图痕迹);
(2)若点Q落在边CD上(C点除外),且∠ADB=n°.
①探究m与n之间的数量关系;
②当点P在线段OB上运动时,存在点Q,使PQ=QD,直接写出n的取值范围.

(1)当点Q与点D重合,请在图中用尺规作出点P所处的位置(不写作法,保留作图痕迹);
(2)若点Q落在边CD上(C点除外),且∠ADB=n°.
①探究m与n之间的数量关系;
②当点P在线段OB上运动时,存在点Q,使PQ=QD,直接写出n的取值范围.
(1)如下图;(2)m+2n=180;(3)30≤n<45
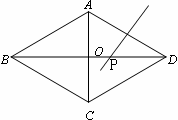

试题分析:(1)作AD的垂直平分线,与BD的交点P即为所求;
(2)①连接PC. 由PC=PQ,得∠3=∠4,根据菱形的性质可得∠3=∠PAD,即可得到∠4=∠PAD,再根据∠4+∠PQD=180°即可求得结果;②根据旋转的性质结合菱形的性质求解即可.
(1)如图所示:

(2)①连接PC. 由PC=PQ,得∠3=∠4
由菱形ABCD得∠3=∠PAD
所以得∠4=∠PAD,
而∠4+∠PQD=180°,
所以∠PAD+∠PQD=180°,
所以m+2n=180;
②30≤n<45.
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
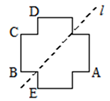


 是方程
是方程 的解;③平行四边形既是中心对称图形又是轴对称图形;④
的解;③平行四边形既是中心对称图形又是轴对称图形;④ 的算术平方根是4。其中真命题的个数有( )
的算术平方根是4。其中真命题的个数有( )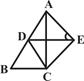
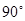 ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.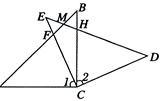
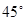 时,试判断四边形ACDM是什么四边形?并证明你的结论.
时,试判断四边形ACDM是什么四边形?并证明你的结论.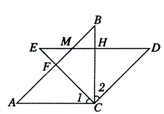

 ,点B、C关于点A成中心对称,则点C所表示的数是__________。
,点B、C关于点A成中心对称,则点C所表示的数是__________。