题目内容
如图,△ABC中,∠C=90°,∠BAC=30°,将△ABC绕点C旋转,使点D落在AB上,连接AE,则sin∠AED= .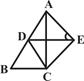

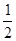
试题分析:根据直角三角形两锐角互余求出∠B=60°,再根据旋转的性质可得BC=CD,∠CDE=∠B,∠CED=∠BAC=30°,然后求出△BCD是等边三角形,根据等边三角形的性质可得∠BCD=60°,然后求出DE∥BC,可得AC⊥DE,再根据直角三角形30°角所对的直角边等于斜边的一半求出BC=
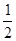 AB,然后求出AD=BD,从而得到DE是AC的垂直平分线,根据对称性求出∠AED=∠CED=30°,最后利用特殊角的锐角三角函数值解答.
AB,然后求出AD=BD,从而得到DE是AC的垂直平分线,根据对称性求出∠AED=∠CED=30°,最后利用特殊角的锐角三角函数值解答.∵∠C=90°,∠BAC=30°,
∴∠B=90°-30°=60°,
∵△EDC是△ABC旋转得到,
∴BC=CD,∠CDE=∠B,∠CED=∠BAC=30°,
∴△BCD是等边三角形,
∴∠BCD=60°,
又∵∠EDC=∠B=60°,
∴DE∥BC,
∴AC⊥DE,
∵∠BAC=30°,∠C=90°,
∴BC=
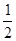 AB,
AB,∴AD=BD=DC,
∴DE是AC的垂直平分线,
根据轴对称性,∠AED=∠CED=30°,
∴sin∠AED=
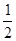 .
.点评:此类问题知识点多,综合性强,难度较大,是中考常见题,需特别注意.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 是等边
是等边 内一点,
内一点, ,
,  .将
.将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转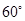 得
得 ,连接
,连接 .
.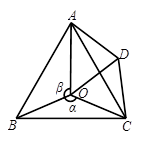
 ,
, 时,试判断
时,试判断 的形状,并说明理由.
的形状,并说明理由. 、
、 的度数.
的度数.