题目内容
已知△ABC中,∠BAC=60゜,D是线段BC上一个动点,以AD为直径画⊙O分别交AB,AC于E、F.
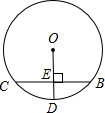
(1)如图1,若AD=4,求EF的长;
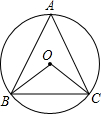
(2)如图2,若∠ABC=45゜,AB=2
,求EF的最小值.

(1)如图1,若AD=4,求EF的长;
(2)如图2,若∠ABC=45゜,AB=2
| 2 |

(1)作直径EP,连结PF,如图1,
∵EP为⊙O的直径,
∴∠EFP=90°,
∵∠P=∠EAF=60°,
∴∠PEF=30°,
∴PF=
PE,
EF=
PF=
EP,
∵EP=AD=4,
∴EF=
×4=2
;
(2)∵EF=
EP=
AD,
∴当AD最小时,EF最小,
当AD⊥BC时,AD最小,如图2,
∵∠ABC=45゜,AB=2
,
∴AD=
AB=2,
∴EF=
×2=
,
即EF的最小值为
.

∵EP为⊙O的直径,
∴∠EFP=90°,
∵∠P=∠EAF=60°,
∴∠PEF=30°,
∴PF=
| 1 |
| 2 |
EF=
| 3 |
| ||
| 2 |
∵EP=AD=4,
∴EF=
| ||
| 2 |
| 3 |
(2)∵EF=
| ||
| 2 |
| ||
| 2 |
∴当AD最小时,EF最小,
当AD⊥BC时,AD最小,如图2,
∵∠ABC=45゜,AB=2
| 2 |
∴AD=
| ||
| 2 |
∴EF=
| ||
| 2 |
| 3 |
即EF的最小值为
| 3 |


练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目