题目内容
如图，已知⊙O的直径AB垂直于弦CD，垂足为E，F为CD延长线上一点，AF交⊙O于点G．
求证：AC2=AG•AF．
求证：AC2=AG•AF．
证明：连接AD、CG，如图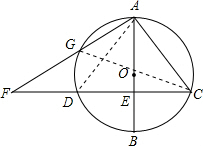
∵直径AB⊥CD，
∴弧AD=弧AC，
∴∠ADC=∠ACF，
∵∠AGC=∠ADC，
∴∠ACF=∠AGC
而∠FAC=∠CAG，
∴△ACG∽△AFC，
∴
=
，
∴AC2=AG•AF．
∵直径AB⊥CD，
∴弧AD=弧AC，
∴∠ADC=∠ACF，
∵∠AGC=∠ADC，
∴∠ACF=∠AGC
而∠FAC=∠CAG，
∴△ACG∽△AFC，
∴
| AC |
| AG |
| AF |
| AC |
∴AC2=AG•AF．
练习册系列答案
寒假学与练系列答案
相关题目
