题目内容
已知关于x的一元二次方程(x﹣m)2+6x=4m﹣3有实数根.
(1)求m的取值范围;
(2)设方程的两实根分别为x1与x2,求代数式x1•x2﹣x12﹣x22的最大值.
(1)求m的取值范围;
(2)设方程的两实根分别为x1与x2,求代数式x1•x2﹣x12﹣x22的最大值.
解:(1)由(x﹣m)2+6x=4m﹣3,得x2+(6﹣2m)x+m2﹣4m+3=0,
∴△=b2﹣4ac=(6﹣2m)2﹣4×1×(m2﹣4m+3)=﹣8m+24。
∵方程有实数根,∴﹣8m+24≥0,解得 m≤3。
∴m的取值范围是m≤3。
(2)∵方程的两实根分别为x1与x2,由根与系数的关系,得
∴x1+x2=2m﹣6,x1·x2= m2﹣4 m+3。
∴x1•x2﹣x12﹣x22="3" x1•x2﹣(x1+x2)2=3(m2﹣4m+3)﹣(2m﹣6)2=﹣m2+12m﹣27
=﹣(m﹣6)2+9。
∵m≤3,且当m<6时,﹣(m﹣6)2+9的值随m的增大而增大,
∴当m=3时,x1•x2﹣x12﹣x22的值最大,最大值为﹣(3﹣6)2+9=0。
∴x1•x2﹣x12﹣x22的最大值是0。
∴△=b2﹣4ac=(6﹣2m)2﹣4×1×(m2﹣4m+3)=﹣8m+24。
∵方程有实数根,∴﹣8m+24≥0,解得 m≤3。
∴m的取值范围是m≤3。
(2)∵方程的两实根分别为x1与x2,由根与系数的关系,得
∴x1+x2=2m﹣6,x1·x2= m2﹣4 m+3。
∴x1•x2﹣x12﹣x22="3" x1•x2﹣(x1+x2)2=3(m2﹣4m+3)﹣(2m﹣6)2=﹣m2+12m﹣27
=﹣(m﹣6)2+9。
∵m≤3,且当m<6时,﹣(m﹣6)2+9的值随m的增大而增大,
∴当m=3时,x1•x2﹣x12﹣x22的值最大,最大值为﹣(3﹣6)2+9=0。
∴x1•x2﹣x12﹣x22的最大值是0。
(1)将原方程转化为关于x的一元二次方程,由于方程有实数根,故根的判别式大于0,据此列不等式解答即可;
(2)将x1•x2﹣x12﹣x22化为两根之积与两根之和的形式,将含m的代数式代入,利用二次函数的最值求解即可。
(2)将x1•x2﹣x12﹣x22化为两根之积与两根之和的形式,将含m的代数式代入,利用二次函数的最值求解即可。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
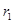 、
、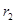 分别是方程
分别是方程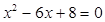 的两实根,若⊙O1与⊙O2的圆心距
的两实根,若⊙O1与⊙O2的圆心距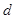 =5.则⊙O1与⊙O2的位置关系是___ _
=5.则⊙O1与⊙O2的位置关系是___ _ 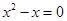 时,只得出一个根x=1,则被漏掉的一个根是
时,只得出一个根x=1,则被漏掉的一个根是

