题目内容
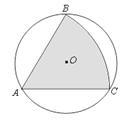
如图,Rt△ABC中,∠C=Rt∠ , D是AB上一点,以BD为圆心的⊙O切AC于点E,交BC于点F ,OG⊥BC于G点。
(1)求证:CE=OG
(2)若BC="3" cm,sinB=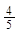 , 求线段AD的长。
, 求线段AD的长。
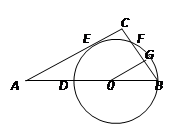
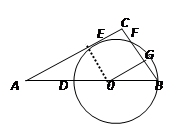
(1)求证:CE=OG
(2)若BC="3" cm,sinB=
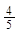 , 求线段AD的长。
, 求线段AD的长。 

(1)证明:连接OE,
∵⊙O切AC于点E ∴∠OEC=900
∵∠ACB=∠CGO=Rt∠
∴四边形OGCE是矩形 ∴CE=OG
(2)解:在Rt△ABC中,sinB=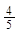
∴cosB=BC/AB=3/5
∵BC="3" ∴AB=BC÷cosB=3×5/3="5" cm
∵∠A=∠A , ∠AEO=∠ACB=Rt∠
∴△AEO∽△ACB
∴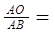
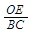 即
即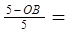
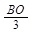
∴OB=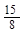
∴DO=2OB=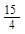
∴AD=AB-DB=5-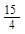 =
=
∵⊙O切AC于点E ∴∠OEC=900
∵∠ACB=∠CGO=Rt∠
∴四边形OGCE是矩形 ∴CE=OG
(2)解:在Rt△ABC中,sinB=
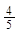
∴cosB=BC/AB=3/5
∵BC="3" ∴AB=BC÷cosB=3×5/3="5" cm
∵∠A=∠A , ∠AEO=∠ACB=Rt∠
∴△AEO∽△ACB
∴
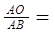
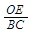 即
即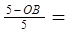
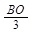
∴OB=
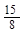
∴DO=2OB=
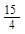
∴AD=AB-DB=5-
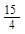 =
=
(1)连接OE,证明四边形OGCE是矩形,从而得出CE=OG;
(2)先利用直角三角形的性质求出AB的长,然后再求圆的半径,从而得出AD的长。
(2)先利用直角三角形的性质求出AB的长,然后再求圆的半径,从而得出AD的长。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

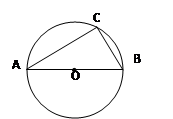
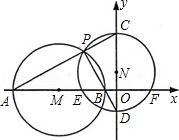
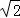 B.等于4
B.等于4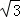 C.等于6 D.随P点
C.等于6 D.随P点