题目内容
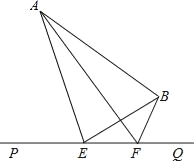
【题目】如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=60°,∠BEQ=45°;在点F处测得∠AFP=45°,∠BFQ=90°,EF=2km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果保留根号).
【答案】(1)AB=AE,理由见解析;(2)(![]() )km.
)km.
【解析】
试题(1)根据SAS即可证明△AEF≌△ABF,得到AB=AE;
(2)作AH⊥PQ,垂足为H.设AE=x,在直角△AHF,直角△AEP中,利用三角函数表示出HE与HF,从而可得到关于x的方程,解方程即可得解.
试题解析:(1)相等.
∵∠BEQ=30°,∠BFQ=60°,
∴∠EBF=∠BEQ=30°,
∴EF=BF,
又∵∠AFP=60°,
∴∠BFA=60°.
在△AEF与△ABF中,
∵ ,
,
∴△AEF≌△ABF(SAS),
∴AB=AE;
(2)过点A作AH⊥PQ,垂足为H.

设AE=xkm,
则AH=xsin60°km,HE=xcos60°km,
∴HF=HE+EF=(xcos60°+2)km,
Rt△AHF中,AH=HFtan45°,
∴AH=HF,
即:xsin60°= xcos60°+2
解得:x=![]() ,
,
即AB=AE=(![]() )km.
)km.
答:两个岛屿A与B之间的距离为(![]() )km.
)km.
考点: 解直角三角形的应用-方向角问题.

练习册系列答案
相关题目