题目内容
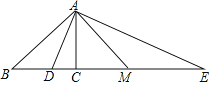
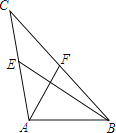
【题目】新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”如图所示,△ABC中AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=6,那么此时AC的长为_____.
【答案】3![]()
【解析】
先利用含30°的直角三角形三边的关系计算出AP=3,BP=3![]() ,再利用中线的定义和重心的性质得到AE=CE,PE=
,再利用中线的定义和重心的性质得到AE=CE,PE=![]() BP=
BP=![]() ,然后利用勾股定理计算AE的长,从而得到AC的长.
,然后利用勾股定理计算AE的长,从而得到AC的长.
解:如图,∵AF⊥BE,
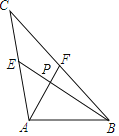
∴∠APB=∠APE=90°,
在Rt△ABP中,∵∠ABP=30°,
∴AP=![]() AB=3,
AB=3,
BP=![]() AP=3
AP=3![]() ,
,
∵AF、BE是中线,
∴AE=CE,点P为△ABC的重心,
∴PE=![]() BP=
BP=![]() ,
,
在Rt△APE中,AE=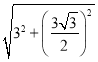 =
=![]() ,
,
∴AC=2AE=3![]() .
.
故答案为3![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】东坡商贸公司购进某种水果成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价P(元/kg)与时间t(天)之间的函数关系式P=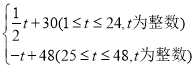 且其日销售量y(kg)与时间t(天)的关系如表下:
且其日销售量y(kg)与时间t(天)的关系如表下:
时间t(天) | 1 | 3 | 6 | 10 | 20 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | … |
(1)已知y与t之间的变化符合一次函数关系,试求在第30天的日销售量.
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,该公司决定每销售1kg水果就捐赠n元利润(0<n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.