题目内容
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
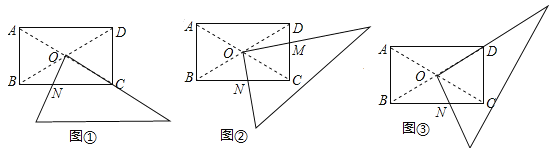
(1)该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;
(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.
(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
【答案】(1)见解析;(2)BN2=NC2+CD2;(3)CM2+CN2=DM2+BN2,理由见解析.
【解析】
(1)连结AN,由矩形知AO=CO,∠ABN=90°,AB=CD,结合ON⊥AC得NA=NC,由∠ABN=90°知NA2=BN2+AB2,从而得证;
(2)连接DN,在Rt△CDN中,根据勾股定理可得:ND2=NC2+CD2,再根据ON垂直平分BD,可得:BN=DN,从而可证:BN2=NC2+CD2;
(3)延长MO交AB于点E,可证:△BEO≌△DMO,NE=NM,在Rt△BEN和Rt△MCN中,根据勾股定理和对应边相等,可证:CN2+CM2=DM2+BN2.
(1)证明:连结AN,
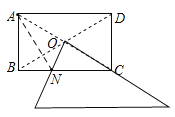
∵矩形ABCD
∴AO=CO,∠ABN=90°,AB=CD,
∵ON⊥AC,
∴NA=NC,
∵∠ABN=90°,
∴NA2=BN2+AB2,
∴NC2=BN2+CD2.
(2)如图2,连接DN.
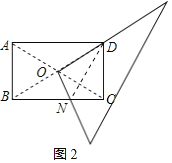
∵四边形ABCD是矩形,
∴BO=DO,∠DCN=90°,
∵ON⊥BD,
∴NB=ND,
∵∠DCN=90°,
∴ND2=NC2+CD2,
∴BN2=NC2+CD2.
(3)CM2+CN2=DM2+BN2
理由如下:延长MO交AB于E,
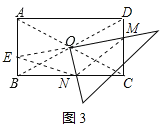
∵矩形ABCD,
∴BO=DO,∠ABC=∠DCB=90°,AB∥CD,
∴∠ABO=∠CDO,∠BEO=∠DMO,
∴△BEO≌△DMO(ASA),
∴OE=OM,BE=DM,
∵MO⊥EM,
∴NE=NM,
∵∠ABC=∠DCB=90°,
∴NE2=BE2+BN2,NM2=CN2+CM2,
∴CN2+CM2=BE2+BN2,
即CN2+CM2=DM2+BN2.

【题目】网上购买鞋子时,消费者需要根据自己脚的情况选择合适的鞋码,每个人千差万别,我们常常会看到下面的表格帮助我们选购:
表1 脚长脚码对应表
脚长(mm) | 220 | 225 | 230 | 235 | 240 | 245 | 250 | 255 | 260 | 265 |
鞋码 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
其中脚长的测量方法是:将脚轻踏于白纸上,在脚趾最长处确定一点,在脚后跟确定一点,测量两点之间的距离,如下图所示
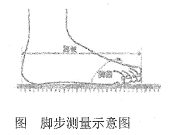
如果一名运动员的脚长是273mm,按上述脚长脚码对应关系他应该穿_________码的鞋子.