题目内容
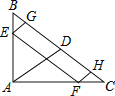
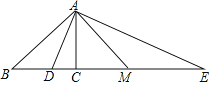
【题目】如图，AD是△ABC中∠BAC的平分线，过A作AE⊥AD交BC的延长线于点E，M为DE的中点．
（1）求证：ME2＝MCMB；
（2）如果BA2＝BDBE，求证：
【答案】（1）见解析；（2）见解析.
【解析】
（1）证明△AMC∽△BMA即可解决问题．
（2）由△AMC∽△BMA，推出
＝
，推出
＝
，推出
＝
，再证明△BAC∽△BMA，推出＝
，推出AB2＝BCBM，即可解决问题．
（1）证明：∵AE⊥AD，
∴∠DAE＝90°，
∵DM＝ME，
∴AM＝MD＝ME，
∴∠MAD＝∠MDA，
∴∠MAC+∠DAC＝∠B+∠BAD，
∵∠BAD＝∠CAD，
∴∠MAC＝∠B，
∵∠AMC＝∠AMB，
∴△AMC∽△BMA，
∴
＝
，
∴AM2＝MCMB，
∵ME＝MA，
∴ME2＝MCMB．
（2）证明：∵△MAC∽△BMA，
∴＝，
∴＝，
∴＝，
∵AB2＝BDBE，
∴
＝
，
∵∠B＝∠B，
∴△BAD∽△BEA，
∴∠BAD＝∠E，
∵∠AMB＝∠E+∠MAE＝2∠E，∠BAC＝2∠BAD，
∴∠BAC＝∠AMB，∵∠B＝∠B，
∴△BAC∽△BMA
∴＝，
∴AB2＝BCBM，
∴＝
＝
．
练习册系列答案
阅读快车系列答案
相关题目
