题目内容
如图,已知A(-4, )、B(2,-4)是一次函数
)、B(2,-4)是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点。
的图象的两个交点。
(1)求反比例函数和一次函数的解析式;
(2)求直线AB和 轴的交点C的坐标及△AOB的面积;
轴的交点C的坐标及△AOB的面积;
(3)求方程 的解(请直接写出答案);
的解(请直接写出答案);
(4)求不等式 的解集(请直接写出答案)。
的解集(请直接写出答案)。

 )、B(2,-4)是一次函数
)、B(2,-4)是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点。
的图象的两个交点。(1)求反比例函数和一次函数的解析式;
(2)求直线AB和
 轴的交点C的坐标及△AOB的面积;
轴的交点C的坐标及△AOB的面积;(3)求方程
 的解(请直接写出答案);
的解(请直接写出答案);(4)求不等式
 的解集(请直接写出答案)。
的解集(请直接写出答案)。
(1) 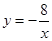 , y="-x-2;" (2) C(-2,0),6.(3)x1=-4,x2=2.(4)-4<x<0或x>2.
, y="-x-2;" (2) C(-2,0),6.(3)x1=-4,x2=2.(4)-4<x<0或x>2.
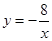 , y="-x-2;" (2) C(-2,0),6.(3)x1=-4,x2=2.(4)-4<x<0或x>2.
, y="-x-2;" (2) C(-2,0),6.(3)x1=-4,x2=2.(4)-4<x<0或x>2.试题分析:(1)由A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数
 的图象的两个交点,利用待定系数法即可求得反比例函数和一次函数的解析式;
的图象的两个交点,利用待定系数法即可求得反比例函数和一次函数的解析式;(2)首先令y=0,即可求得x的值,则可得直线AB与x轴的交点C的坐标,然后由S△AOB=S△AOC+S△BOC,求得三角形AOB的面积;
(3)求方程
 的解即是求函数y=kx+b以函数
的解即是求函数y=kx+b以函数 的交点的横坐标.
的交点的横坐标.(4)观察图象结合(3)即可求不等式
 的解集.
的解集.试题解析:(1)∵B(2,-4)在函数
 的图象上,
的图象上,∴m=-8.
∴反比例函数的解析式为:
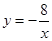 .
.∵点A(-4,n)在函数
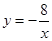 的图象上,
的图象上,∴n=2,
∴A(-4,2),
∵y=kx+b经过A(-4,2),B(2,-4),
∴
 ,解之得:
,解之得: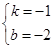 .
.∴一次函数的解析式为:y=-x-2.
(2)∵C是直线AB与x轴的交点,∴当y=0时,x=-2.
∴点C(-2,0),
∴OC=2.
∴S△AOB=S△ACO+S△BCO=
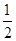 OC•n+
OC•n+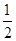 OC×4=
OC×4=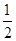 ×2×2+
×2×2+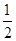 ×2×4=6.
×2×4=6.(3)x1=-4,x2=2.
(4)-4<x<0或x>2.

练习册系列答案
相关题目

 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标;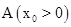 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
 与直线
与直线 交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程
交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程 的解为
的解为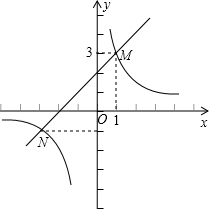
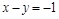 的解为坐标的点在平面直角坐标系中的图象是一条直线。根据这个结论,在同一平面直角坐标系中画出二元一次方程组
的解为坐标的点在平面直角坐标系中的图象是一条直线。根据这个结论,在同一平面直角坐标系中画出二元一次方程组 中两个二元一次方程的图象,并根据图象写出这个二元一次方程组的解。
中两个二元一次方程的图象,并根据图象写出这个二元一次方程组的解。 随着所处深度
随着所处深度 的变化而变化,在某个地点
的变化而变化,在某个地点 来表示,则
来表示,则