Question

【题目】抛物线y＝﹣x2+2x+8与x轴交于B、C两点，点D平分BC，且点A为抛物线上的点，且∠BAC为锐角，则AD的值范围为_____．

Answer 1

【答案】3＜x≤9

【解析】

由“∠BAC为锐角”可知点A在以定线段BC为直径的圆外，又点A在x轴上侧，从而可确定动点A的范围．

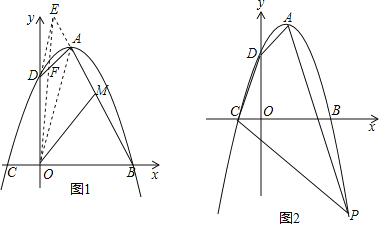
解：如图，∵抛物线y＝﹣x2+2x+8，

∴抛物线的顶点为A0(1，9)，

对称轴为x＝1，

与x轴交于两点B(﹣2，0)、C(4，0)，

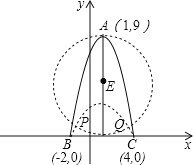
分别以BC、DA为直径作⊙D、⊙E，则

两圆与抛物线均交于两点P(1﹣2，1)、Q(1+2，1)．

可知，点A在不含端点的抛物线内时，∠BAC＜90°，

且有3＝DP＝DQ＜AD≤DA0＝9，即AD的取值范围是3＜AD≤9．

则A的横坐标取值范围是3＜x≤9．

故答案为：3＜x≤9．