题目内容
【题目】已知在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点
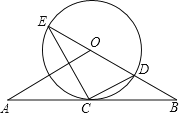
(1)如图1,BE交⊙O于点F,求证:∠EFC=∠BFD;
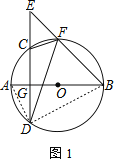
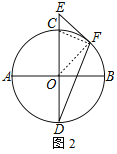
(2)如图2,当CD也是直径,EF切⊙O于F,连接DF.若tan∠D=![]() ,求sin∠E的值.
,求sin∠E的值.

【答案】(1)见解析;(2)![]()
【解析】
(1)连接AD,BD,由圆的性质可得∠CFE=∠EDB,再证明∠ADB=∠AGD=90°,可得∠DAB=∠GDB,则∠EFC=∠BFD得证;
(2)证明△CEF∽△FED,可得EF2=CEDE,设CF=a,则DF=3a,由勾股定理可得CD=![]() ,设CE=x,则EF=3x,可求出CE=
,设CE=x,则EF=3x,可求出CE=![]() 和EF=
和EF=![]() ,可用a表示OF的长,则sin∠E的值可求出.
,可用a表示OF的长,则sin∠E的值可求出.
(1)证明:如图1,连接AD,BD,
∵四边形CDBF为圆内接四边形,
∴∠CFE=∠EDB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵AB⊥CD,
∴∠AGD=90°,
∴∠GDB+∠ABD=90°,
∴∠DAB=∠GDB,
∴∠DAB=∠CFE,
∵∠DAB=∠BFD,
∴∠EFC=∠BFD;
(2)解:如图2,连接OF,CF,
∵EF是⊙O的切线,
∴OF⊥EF,
∴∠EFO=90°,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴∠EFC=∠OFD,
∵OF=OD,
∴∠ODF=∠OFD,
∴∠ODF=∠EFC,
∵∠CEF=∠FED,
∴△CEF∽△FED,
∴![]() ,
,
∴EF2=CEDE,
∵tan∠D=![]() =
=![]() ,
,
设CF=a,则DF=3a,由勾股定理可得CD=![]() ,
,
设CE=x,则EF=3x,
∴![]() ,
,
解得:x=![]() ,
,
∴![]() ,
,
∴OE=CE+OC=![]() ,
,
∴![]() =
=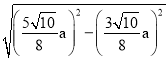 =
=![]() ,
,
∴sin∠E=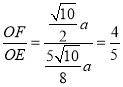 .
.

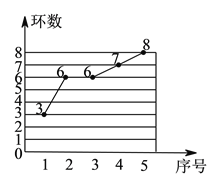
【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛,故先在射击队举行了一场选拔比赛.在相同的条件下各射靶![]() 次,每次射靶的成绩情况如图所示.
次,每次射靶的成绩情况如图所示.
甲射靶成绩的条形统计图
| 乙射靶成绩的折线统计图
|
(![]() )请你根据图中的数据填写下表:
)请你根据图中的数据填写下表:
平均数 | 众数 | 方差 | |
甲 | __________ |
|
|
乙 |
| __________ | __________ |
(![]() )根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
)根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.