题目内容
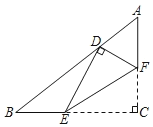
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则BD的长为__________.
【答案】![]() 或
或![]() .
.
【解析】
连接CD,先根据折叠的性质得出![]() ,再根据△EFC和△ABC相似,分两种情况讨论:当
,再根据△EFC和△ABC相似,分两种情况讨论:当![]() 时,先推出CD⊥AB,进而根据同角三角函数相等得出
时,先推出CD⊥AB,进而根据同角三角函数相等得出![]() 的值;当
的值;当![]() 时,先推出
时,先推出![]() ,
,![]() ,进而根据等角对等边求解.
,进而根据等角对等边求解.
∵在Rt△ABC中,∠ACB=90°,AB=5,BC=4,
∴![]() ,
,
若△CEF与△ABC相似,分两种情况:
①当![]() 时,EF∥AB,
时,EF∥AB,
连接CD,如图1所示:

∵由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高,
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,
∴cosB![]() ,
,
∵在Rt△BDC中,cosB![]() ,
,
∴BD=BCcosB=4![]() ;
;
②当![]() 时,∠CEF=∠A,
时,∠CEF=∠A,
连接CD,如图2所示:

∵由折叠性质可知,CD⊥EF,
∴∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠B=∠ECD,
∴BD=CD,
同理可得:∠A=∠FCD,AD=CD,
∴D点为AB的中点,
∴BD![]() AB
AB![]() ,
,
故答案为:![]() 或
或![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人、2人、3人、4人、5人分别记为A、B、C、D、E,由调查所得数据绘制了如图所示的不完整的统计图表.
类别 | 频率 |
A | m |
B | 0.35 |
C | 0.20 |
D | n |
E | 0.05 |
(1)求本次调查的小型汽车数量及m,n的值;
(2)补全频数分布直方图;

(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中每车只乘坐1人的小型汽车数量.