题目内容
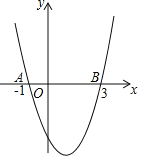
【题目】如图,一次函数与x轴,y轴的交点分别是A(﹣4,0),B(0,2).与反比例函数的图象交于点Q,反比例函数图象上有一点P满足:①PA⊥x轴;②PO=![]() (O为坐标原点),则四边形PAQO的面积为( )
(O为坐标原点),则四边形PAQO的面积为( )

A.7B.10C.4+2![]() D.4﹣2
D.4﹣2![]()
【答案】C
【解析】
利用待定系数法求解函数解析式,求出P点的坐标,然后用待定系数法即可求出函数解析式;解方程组得到点Q的坐标,然后根据三角形的面积公式即可得到结论.
解:∵一次函数y=ax+b与x轴,y轴的交点分别是A(﹣4,0),B(0,2),
∴﹣4a+b=0,b=2,
∴a=![]() ,
,
∴一次函数的关系式为y=![]() x+2,
x+2,
设P(﹣4,n),
∴![]() ,
,
解得:n=±1,
由题意知n=﹣1,n=1(舍去),
∴把P(﹣4,﹣1)代入反比例函数y=![]() ,
,
∴m=4,
反比例函数的关系式为:y=![]() ,
,
解 得,
得, ,
,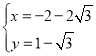 (舍去),
(舍去),
∴Q(﹣2+2![]() ,
,![]() +1),
+1),
∴四边形PAQO的面积=![]() ×4×1+
×4×1+![]() 4×2+
4×2+![]() 2×(﹣2+2
2×(﹣2+2![]() )=4+2
)=4+2![]() ,
,
故选:C.

【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.

运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | b | 7 | 5 | 8 | a | 8 | 7 |
(1)若运动员丙测试成绩的平均数和众数都是7,则成绩表中的a= ,b= ;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为S甲2=0.81、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,第二轮结束时球又回到乙手中的概率是多少?(用树状图或列表法解答)
【题目】某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人、2人、3人、4人、5人分别记为A、B、C、D、E,由调查所得数据绘制了如图所示的不完整的统计图表.
类别 | 频率 |
A | m |
B | 0.35 |
C | 0.20 |
D | n |
E | 0.05 |
(1)求本次调查的小型汽车数量及m,n的值;
(2)补全频数分布直方图;

(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中每车只乘坐1人的小型汽车数量.