题目内容
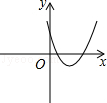
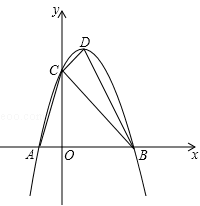
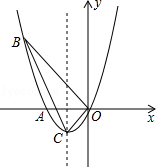
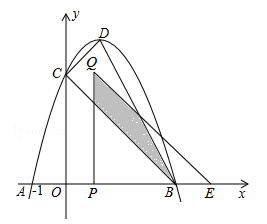
抛物线y=﹣x2平移后的位置如图所示,点A,B坐标分别为(﹣1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.
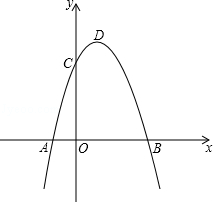
(1)求平移后的抛物线的解析式和点D的坐标;
(2)∠ACB和∠ABD是否相等?请证明你的结论;
(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.

(1)求平移后的抛物线的解析式和点D的坐标;
(2)∠ACB和∠ABD是否相等?请证明你的结论;
(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.
解:(1)∵将抛物线y=﹣x2平移,平移后的抛物线与x轴交于点A(﹣1,0)和点B(3,0),
∴平移后的抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,即y=﹣x2+2x+3。
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4)。
(2)∠ACB与∠ABD相等。理由如下:
如图,∵y=﹣x2+2x+3,
∴当x=0时,y=3,即C点坐标为(0,3)。
又∵B(3,0),∠BOC=90°,
∴OB=OC,∠OBC=∠OCB=45°。
在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,
∴BC2+CD2=BD2。∴∠BCD=90°。
∴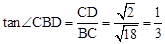 。
。
∵在△AOC中,∠AOC=90°,∴tan∠ACO=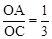 。
。
∴tan∠ACO=tan∠CBD。∴∠ACO=∠CBD。
∴∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD。
(3)∵点P在平移后的抛物线的对称轴上,而y=﹣x2+2x+3的对称轴为x=1,
∴可设P点的坐标为(1,n)。
∵△ABC是锐角三角形,∴当△CDP与△ABC相似时,△CDP也是锐角三角形。
∴n<4,即点P只能在点D的下方。
又∵∠CDP=∠ABC=45°,∴D与B是对应点,分两种情况:
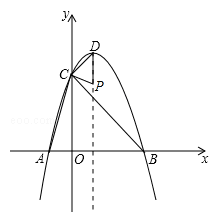
①如果△CDP∽△ABC,那么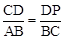 ,
,
即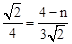 。解得n=
。解得n=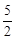 ,
,
∴P点的坐标为(1,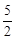 )。
)。
②如果△CDP∽△CBA,那么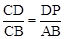 ,
,
即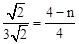 ,解得n=
,解得n=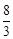 。
。
∴P点的坐标为(1,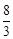 )。
)。
综上可知P点的坐标为(1,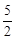 )或(1,
)或(1,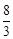 )。
)。
∴平移后的抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,即y=﹣x2+2x+3。
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4)。
(2)∠ACB与∠ABD相等。理由如下:
如图,∵y=﹣x2+2x+3,

∴当x=0时,y=3,即C点坐标为(0,3)。
又∵B(3,0),∠BOC=90°,
∴OB=OC,∠OBC=∠OCB=45°。
在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,
∴BC2+CD2=BD2。∴∠BCD=90°。
∴
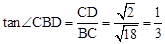 。
。∵在△AOC中,∠AOC=90°,∴tan∠ACO=
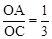 。
。∴tan∠ACO=tan∠CBD。∴∠ACO=∠CBD。
∴∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD。
(3)∵点P在平移后的抛物线的对称轴上,而y=﹣x2+2x+3的对称轴为x=1,
∴可设P点的坐标为(1,n)。
∵△ABC是锐角三角形,∴当△CDP与△ABC相似时,△CDP也是锐角三角形。
∴n<4,即点P只能在点D的下方。
又∵∠CDP=∠ABC=45°,∴D与B是对应点,分两种情况:

①如果△CDP∽△ABC,那么
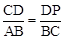 ,
,即
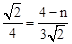 。解得n=
。解得n=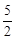 ,
,∴P点的坐标为(1,
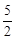 )。
)。②如果△CDP∽△CBA,那么
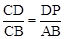 ,
,即
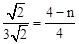 ,解得n=
,解得n=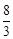 。
。∴P点的坐标为(1,
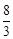 )。
)。综上可知P点的坐标为(1,
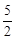 )或(1,
)或(1,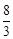 )。
)。试题分析:(1)根据平移不改变二次项系数a的值,且平移后的抛物线与x轴交于点A(﹣1,0)和点B(3,0),可知平移后抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,再运用配方法化为顶点式,即可求出顶点D的坐标。
(2)先由B、C两点的坐标,得出∠OBC=∠OCB=45°,再根据勾股定理的逆定理判断△BCD是直角三角形,且∠BCD=90°,则由正切函数的定义求出tan∠CBD=
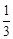 ,在△AOC中,由正切函数的定义也求出tan∠ACO=
,在△AOC中,由正切函数的定义也求出tan∠ACO=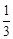 ,得出∠ACO=∠CBD,则∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD。
,得出∠ACO=∠CBD,则∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD。(3)设P点的坐标为(1,n),先由相似三角形的形状相同,得出△CDP是锐角三角形,则n<4,再根据∠CDP=∠ABC=45°,得到D与B是对应点,所以分两种情况进行讨论:
①△CDP∽△ABC;
②△CDP∽△CBA。
根据相似三角形对应边的比相等列出关于n的方程,解方程即可。

练习册系列答案
相关题目
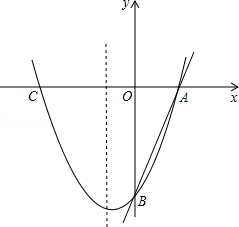
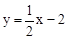 与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).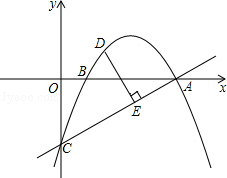
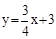 的图象与y轴的交点,点B在二次函数
的图象与y轴的交点,点B在二次函数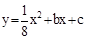 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.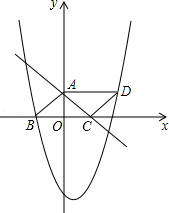
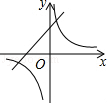
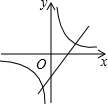
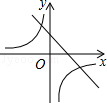
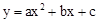 的图象如图所示,则一次函数
的图象如图所示,则一次函数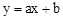 与反比例函数
与反比例函数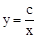 在同一平面直角坐标系中的大致图象为【 】
在同一平面直角坐标系中的大致图象为【 】