题目内容
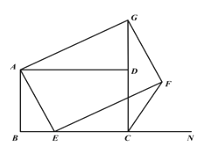
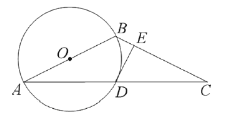
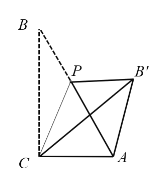
【题目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,点P是AB上一点,连接CP,将∠B沿CP折叠,使点B落在B'处.以下结论正确的有________
①当AB'⊥AC时,AB'的长为![]() ;
;
②当点P位于AB中点时,四边形ACPB'为菱形;
③当∠B'PA=30°时,![]() ;
;
④当CP⊥AB时,AP:AB':BP=1:2:3.
【答案】①②④
【解析】
由折叠的性质及直角三角形的性质对结论一一判断即可.
解:①AC=1,∠B=30°可知BC=![]() ,由翻折可知:B′C=BC=
,由翻折可知:B′C=BC=![]() ,
,
因为AB'⊥AC,由勾股定理可知:
AB'=![]() =
=![]() ,正确.
,正确.
②当点P位于AB中点时,CP=PB=PA=AC=PB′,∠B'PA=PAC=60°,PB'∥AC,
所以四边形ACPB'是平行四边形,
又PC=AC,
所以四边形ACPB'是菱形,正确.
③当∠B'PA=30°时,可知四边形BCB′P是菱形,BP=BC=![]() ;AP=2-
;AP=2-![]() ,
,
![]() 成立,故不正确.
成立,故不正确.
④当CP⊥AB时,∠B'=∠B'CA=30°,AC=AB',∠ACP=∠B=30°,
设AP=a,则AB'=AC=2a;AB=4a,PB=3a;
所以:AP:AB':BP=a:2a:3a=1:2:3,正确.
故答案为:①②④.

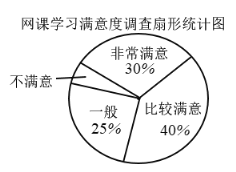
【题目】王老师从本校九年级质量检测的成绩中随机地抽取一些同学的数学成绩做质量分析,他先按照等级绘制这些人数学成绩的扇形统计图,如图(1)所示,数学成绩等级标准见表1,又按分数段绘制成绩分布表,如表2,
表1
等级 | 分数x的范围 |
A | a≤x≤100 |
B | 80≤x<a |
C | 60≤x<80 |
D | 0≤x<60 |
表2
分数段 | x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
人数 | 5 | 10 | m | 12 | n |
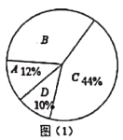
分数段为90≤x≤100的n个人中,其成绩的中位数是95分.
根据以上信息回答下面问题:
(1)王老师抽查了多少人?m、n的值分别是多少;
(2)小明在此考试中得了95分,他说自己在这些考试中数学成绩是A等级,他说的对吗?为什么?
(3)若此次测试数学学科普高的预测线是70分,该校九年级有900名学生,求数学学科达到普高预测线的学生约有多少人?
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
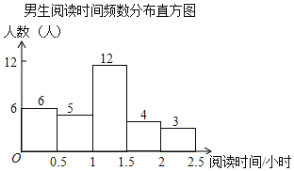
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?
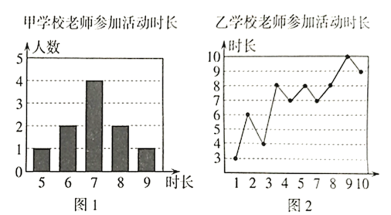
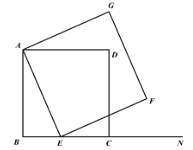
【题目】甲、乙两所学校选派相同人数的老师参加志愿者活动,參加活动时长分别被制成下列两个统计图,根据以上信息,整理分析数据如下表:
平均时间/小时 | 中位数/小时 | 众数/小时 | 方差/小时 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
![]() 求出表格中
求出表格中![]() 的值.
的值.
![]() 分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?
分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?