题目内容
【题目】如图，直线
与二次函数
的图象交于点B、点C，二次函数图象的顶点为A，当
是等腰直角三角形时，则
______．
【答案】1
【解析】
作抛物线的对称轴，交BC于D，根据抛物线的性质和等腰直角三角形的性质得出B（n+3，n），代入解析式求得即可．
作抛物线的对称轴，交BC于D，
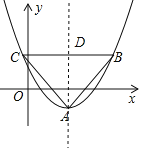
∵直线y=n与二次函数y=
（x-2）2-1的图象交于点B、点C，
∴BC∥x轴，
∵△ABC是等腰直角三角形，
∴∠CAB=90°，AC=BC，
∵直线CD是抛物线的对称轴，
∴AD⊥BC，∠CAD=∠BAD=45°，
∴△ADB是等腰直角三角形，
∴AD=BD，
∵抛物线的顶点为（2，-1），
∴AD=n+1，
∴B（n+3，n），
把B的坐标代入y=（x-2）2-1得，n=（n+3-2）2-1，
解得n=1，
故答案为1．
练习册系列答案
相关题目
