Question

【题目】对称变换和平移变换在平面几何中有着广泛的应用，特别是在解决有关最值问题时，更是我们常用的思维方法，请你利用所学知识解决下列问题：

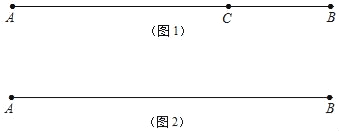
（1）如图①，在平面直角坐标系中，已知点A（0，1），点B（2，1），点P在x轴上运动，当PA+PB的值最小时，点P的坐标是　　；（请直接写出答案）

（2）如图②，AD⊥l于点D，BC⊥l于点C，且AD＝2，AB＝BC＝4，当点P在直线l上运动时，PA+PB的最小值是　　；（请直接写出答案）

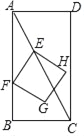
（3）如图③，直线a∥b，且a与b之间的距离为1，点A到直线a的距离为2，点B到直线b的距离为2，且AB＝，问：在直线a上是否存在点C，在直线b上是否存在点D，使得CD⊥a，且AC+CD+DB的值最小？若存在，请求出AC+CD+DB的最小值；若不存在，请说明理由．

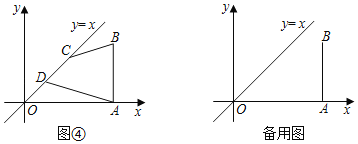
（4）如图④，在平面直角坐标系中，A（6，0），B（6，4），线段CD在直线y＝x上运动，且CD＝2，则四边形ABCD周长的最小值是　，此时点D的坐标为　．（请直接写出答案）

Answer 1

【答案】（1）（1，0）；（2）4；（3）存在，6；（4）6+4，（3，3）

【解析】

（1）如图1，作点A关于x轴的对称点，连接 交x轴于点P，则点P为所求点，然后利用待定系数法求出直线的解析式，然后令 即可求出x的值，从而可确定P的坐标；

（2）如图2，作点A关于直线l的对称点，连接交直线l于点P，则点P为所求点，利用矩形的性质和勾股定理进而求解即可；

（3）如图3，将点A向下平移1个单位得到，连接交直线b于点D，过点D作DC⊥a于点C，连接AC，则点C、D为所求点，然后利用勾股定理求出的长度，进而求解；

（4）如图4，将点A沿y＝x方向向右平移2个单位得到，作点关于直线y＝x的对称点，连接交直线y＝x于点C，将点C沿直线向下平移2个单位得到点C，则点C、D为所求点，首先利用平行四边形的性质得出四边形ABCD周长＝4+2+为最小，然后利用勾股定理即可求出的值，进而可求出周长的最小值，然后利用待定系数法求出直线的解析式，进而可求出C的坐标，从而D的坐标可求 ．

解：（1）如图1，作点A关于x轴的对称点，连接交直线l于点P，则点P为所求点，

∵点 、A关于x轴对称，，

， ，

∴为最小；

设直线的表达式为：y＝kx+b，

将点 代入得

，解得：，

故直线的表达式为：y＝x﹣1，

当y＝0时，x＝1，故点P（1，0）；

故答案为：（1，0）；

（2）如图2，作点A关于直线l的对称点，连接交直线l于点P，则点P为所求点，过点作交BC的延长线于点H，

∵点 、A关于x轴对称，

，

∴为最小；

过点A作AM⊥BC于点M，

，

∴ ，

∴四边形ADCM是矩形，

∴，

同理， ，

∴BM＝BC﹣CM＝BC﹣AD＝4﹣2＝2．

在Rt△ABM中，AM2＝AB2﹣BM2＝16﹣4＝12＝ ，

BH＝CH+BC＝+BC＝2+4＝6，

在中，

；

即PA+PB的最小值为4，

故答案为：4；

（3）存在，理由：

如图3，将点A向下平移1个单位得到，连接交直线b于点D，过点D作DC⊥a于点C，连接AC，则点C、D为所求点，

∵，且，

∴四边形为平行四边形，

∴，

∴ 为最小．

过点 、A分别作直线a的平行线，分别交过点B与a的垂线于点G、H，则四边形为矩形，

∵BH＝2+1+2＝5，AB＝，则AH＝＝3，

在中，，BG＝2+1+1＝4，

，

∴，

∴AC+CD+DB最小值为6；

（4）如图4，将点A沿y＝x方向向右平移2个单位长度得到，作点关于直线y＝x的对称点，连接交直线y＝x于点C，将点C沿直线向下平移2个单位长度得到点D，则点C、D为所求点．

连接AD、，

设C的坐标为 ，

∵ ，

，

，

∴如果沿着直线向上平移个单位长度，相当于向右平移2个单位，再向上平移2个单位．

∵，

．

∵点和点关于对称，

．

∵，

∴四边形为平行四边形，

∴．

，

．

，

，

∴四边形ABCD周长＝AB+CD+BC+AD＝AB+CD+BC+＝4+2+为最小．

∵=＝4，

故四边形ABCD周长最小值为：64．

设直线的解析式为，

将代入解析式中得

解得

∴直线解析式为 ．

，解得：，

故点C（5，5），

而CD＝2，

∴点D可以看成点C向左平移2个单位长度，再向下平移2个单位长度得到的，

∴点D（3，3），

故答案为：6+4；（3，3）．