题目内容
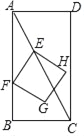
【题目】如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒![]() 个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
(1)用含t的代数式表示点E到边AB的距离.
(2)当点G落在边AB上时,求t的值.
(3)连结BG,设△BFG的面积为S平方单位(S>0),求S与t之间的函数关系式.
(4)直接写出当正方形EFGH的顶点与点B,D距离相等时的t值.
【答案】(1)点E到边AB的距离为t(2)t=1(3)S=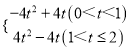 (4)当正方形EFGH的顶点与点B,D距离相等时的t值为
(4)当正方形EFGH的顶点与点B,D距离相等时的t值为![]() s或1s或
s或1s或![]() s
s
【解析】试题分析:(1)如图1中,作EM⊥AB于M.由EM∥BC,可得![]() ,即
,即![]() ,延长即可解决问题;
,延长即可解决问题;
(2)如图2中,G在AB边时,由AF+FB=4,可得2t+2t=4,解方程即可;
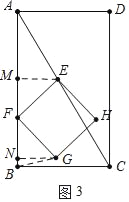
(3)分两种情形①如图3中,当0<t<1时,作GN⊥AB于N,EM⊥AB于M.②如图4中,当1<t≤2时,作GN⊥AB于N,EM⊥AB于M.分别求解即可;
(4)分三种情形①如图5中,当H在BD的垂直平分线上时,根据HD=HB列出方程即可解决问题;②当点E在BD的垂直平分线上时,易知AE=EC,t=1;③当点F在线段BD的垂直平分线上时,分别求解即可.
试题解析:(1)如图1中,作EM⊥AB于M.
∵AB=4,BC=2,∠B=90°,
∴AC=![]() ,
,
∵EM∥BC,
∴![]() ,
,
∴![]() ,
,
∴EM=t,AM=2t.
∴点E到边AB的距离为t.
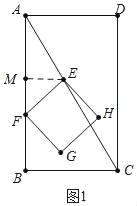
(2)如图2中,G在AB边时,
由AF+FB=4,可得2t+2t=4,
∴t=1.
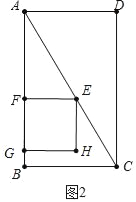
(3)①如图3中,当0<t<1时,作GN⊥AB于N,EM⊥AB于M.
由△EMF≌△FNG,可得NG=FM=4﹣4t,
∴S=![]() FBGN=
FBGN=![]() 2t(4﹣4t)=﹣4t2+4t.
2t(4﹣4t)=﹣4t2+4t.
②如图4中,当1<t≤2时,作GN⊥AB于N,EM⊥AB于M.
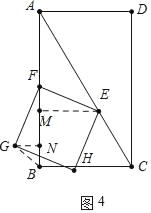
由△EMF≌△FNG,可得NG=FM=4t﹣4
S=![]()
![]() 2t(4t﹣4)=4t2﹣4t.
2t(4t﹣4)=4t2﹣4t.
综上所述,S=![]() .
.
(4)①如图5中,当H在BD的垂直平分线上时,
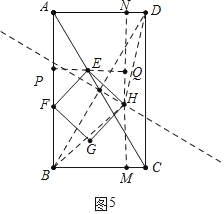
作HM⊥BC于M,延长MH交AD于N,作EP⊥AB于P,延长PE交MN于Q.
由△EPF≌△HQE可得HQ=EP=T.EQ=PF=4﹣4t,
在Rt△HND中,DH2=DN2+HN2=(3t﹣2)2+(3t)2,
在Rt△BHM中,BH2=(4﹣3t)2+(4﹣3t)2,
∴HD=HB,
∴(3t﹣2)2+(3t)2=4﹣3t)2+(4﹣3t)2,
∴t=![]() .
.
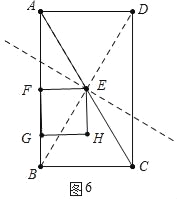
②当点E在BD的垂直平分线上时,易知AE=EC,t=1.
③当点F在线段BD的垂直平分线上时,
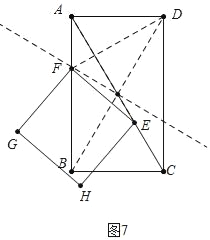
∵BF=DF=2t
在Rt△ADF中,22+(4﹣2t2=(2t)2,
∴t=![]() ,
,
综上所述,当正方形EFGH的顶点与点B,D距离相等时的t值为![]() s或1s或
s或1s或![]() s.
s.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案