题目内容
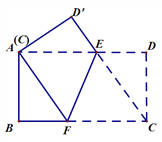
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=90°,AD=CD+AB,∠BAC=45°,E是BC上一点,且∠DAE=45°,若BC=8,则△ADE面积为__.

【答案】![]()
【解析】
过点A作CD的垂线,交CD的延长线于点F,可得四边形ABCF是正方形,设CD=m,根据勾股定理可求出m=2,将△ABE绕点A顺时针旋转90°至△AFG,可以证明△ADE≌△ADG,设BE=n,再根据勾股定理可求DG的长,进而可得△ADG的面积,即可得△ADE的面积.
解:如图,过点A作CD的垂线,交CD的延长线于点F,

![]() ,
,
![]() ,
,
![]() .
.
![]()
∴四边形ABCF是矩形.
∵∠ABC=90°,∠BAC=45°,
∴AB=BC,
∴四边形ABCF是正方形,
∴AB=BC=AF=CF=8,
设CD=m,
则AD=CD+AB=m+8,DF=CF﹣CD=8﹣m,
在Rt△AFD中,根据勾股定理,得
(m+8)2=(8﹣m)2+82,
解得m=2,
∴FD=6,AD=10,
将△ABE绕点A顺时针旋转90°至△AFG,
∴AG=AE,BE=FG,∠EAG=∠BAF=90°,
∵∠BAC=45°,∠DAE=45°,
∴∠BAE=∠DAC,
∴∠CAE=∠DAF,
∵∠BAE=∠FAG,
∴∠DAE=∠DAG,
AD=AD,
∴△ADE≌△ADG(SAS),
∴DE=DG,
设BE=n,则CE=BC﹣BE=8﹣n,DE=DG=DF+FG=DF+BE=6+n,
在Rt△DCE中,根据勾股定理,得
(6+n)2=(8﹣n)2+22
解得n=![]() ,
,
∴DG=6+![]() =
=![]() ,
,
∴S△ADE=S△ADG=![]() DG×AF=
DG×AF=![]() ×8=
×8=![]() .
.
故答案为:![]() .
.

【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
【题目】某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了统计表如下:

零花钱数额(元) | 5 | 10 | 15 | 20 |
学生个数(个) | a | 15 | 20 | 5 |
请根据表中的信息,回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱额的众数、中位数和平均数.