Question

【题目】已知ABC为等边三角形，点D、E分别在直线AB、BC上，且AD=BE.

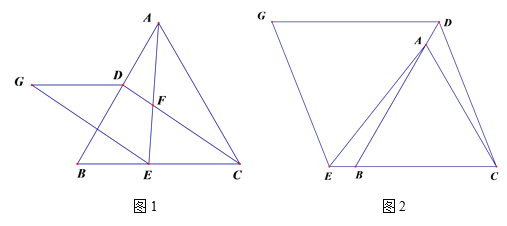
（1）如图1，若点D、E分别是AB、CB边上的点，连接AE、CD交于点F，过点E作∠AEG=60°，使EG=AE，连接GD，则∠AFD= （填度数）；

（2）在（1）的条件下，猜想DG与CE存在什么关系，并证明；

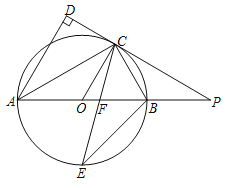
（3）如图2，若点D、E分别是BA、CB延长线上的点，（2）中结论是否仍然成立？请给出判断并证明.

Answer 1

【答案】(1)∠AFD= 60°（2）DG=CE，DG//CE；（3）详见解析

【解析】

(1) 证明△ABE≌△CAD(SAS)，可得 ∠BAE=∠ACD，继而根据等边三角形的内角为60度以及三角形外角的性质即可求得答案；

(2)由(1)∠AFD=60°，根据∠AEG=60°，可得GE//CD ，继而根据GE=AE=CD，可得四边形GECD是平行四边形，根据平行四边形的性质即可得DG=CE，DG//CE；

(3)延长EA交CD于点F，先证明△ACD≌△BAE，根据全等三角形的性质可得 ∠ACD=∠BAE， CD=AE，继而根据三角形外角的性质可得到∠EFC= 60°，从而得∠EFC=∠GEF，得到GE//CD，继而证明四边形GECD是平行四边形 ，根据平行四边形的性质即可得到DG=CE，DG//CE.

(1) ∵△ABC是等边三角形，

∴AB=AC，∠BAC=∠ABC=60°，

在△ABE和△CAD中，

，

∴△ABE≌△CAD(SAS)，

∴∠BAE=∠ACD，

∵∠BAE+∠EAC=∠BAC=60°，

∴∠ACD+∠EAC=60°，

∴∠AFD=∠ACD+∠EAC=60°，

故答案为：60° ；

(2)DG=CE，DG//CE，理由如下：

∵△ABC是等边三角形，

∴AB=AC，∠BAC=∠ABC=60°，

在△ABE和△CAD中，

，

∴△ABE≌△CAD(SAS)，

∴AE=CD，∠BAE=∠ACD，

∵∠BAE+∠EAC=∠BAC=60°，

∴∠ACD+∠EAC=60°，

∴∠AFD=∠ACD+∠EAC=60°，

又∵∠AEG=60°，

∴∠AFD=∠AEG，

∴GE//CD ，

∵GE=AE=CD，

∴四边形GECD是平行四边形，

∴DG=CE，DG//CE；

(3)仍然成立

延长EA交CD于点F，

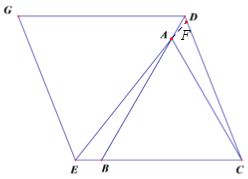
∵△ABC为等边三角形，

∴AC=AB，∠BAC=∠ABC=60°，

∴∠DAC=∠ABE=120°，

在△ACD和△BAE中，

，

∴△ACD≌△BAE(SAS)，

∴∠ACD=∠BAE， CD=AE，

∴∠EFC=∠DAF+∠BDC=∠BAE +∠AEB=∠ABC= 60°，

∴∠EFC=∠GEF，

∴GE//CD，

∵GE=AE=CD，

∴四边形GECD是平行四边形 ，

∴DG=CE，DG//CE.