题目内容
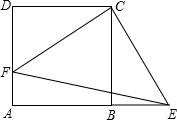
在△ABC中,∠C=90°,∠A,∠B的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:四边形CFDE是正方形.


证明:过点D作DG⊥AB,垂足为G,
∵∠CFD=∠CED=∠C=90°,
∴四边形CEDF是矩形.
∵AD,BD分别是∠CAB,∠CBA的平分线,
∴DF=DG,DG=DE.
∴DF=DE.
∴四边形CFDE是正方形.

∵∠CFD=∠CED=∠C=90°,
∴四边形CEDF是矩形.
∵AD,BD分别是∠CAB,∠CBA的平分线,
∴DF=DG,DG=DE.
∴DF=DE.
∴四边形CFDE是正方形.


练习册系列答案
相关题目