题目内容
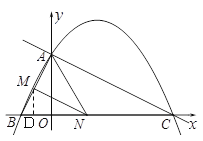
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.

【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)△ABC是直角三角形(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4
x+4;(2)△ABC是直角三角形(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0)(4)当△AMN面积最大时,N点坐标为(3,0)
,0)(4)当△AMN面积最大时,N点坐标为(3,0)
【解析】
试题(1)由A点坐标确定解析式中c值,再把C点坐标代入解析式求出a值,从而确定此解析式;(2)根据解析式求出B点坐标,在Rt△AOB中,利用勾股定理求出AB,在Rt△AOC中,利用勾股定理求出AC,然后利用勾股定理的逆定理验证△ABC是直角三角形;(3)满足△ANC为等腰三角形的N点有四个,在x轴负半轴有两点,满足AN=AC,AC=NC,在x轴正半轴存在两点,满足AN=CN,AC=NC,然后先求出AC长,利用等腰三角形两腰相等,和勾股定理易求出N点横坐标,因为N在x轴上,所以纵坐标是0,从而得到N点坐标.(4)先找到自变量,设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,利用平行线分线段成比例定理和三角形相似把MD用n表示出来,这样△AMN的面积就用△ABN的面积减去△BMN的面积,从而建立S与n的二次函数,讨论n的取值及函数最大值,即可求出△AMN面积最大时,点N的坐标.
试题解析:(1)∵A(0,4),∴c=4,,把点C坐标(8,0)代入解析式,得:a=-![]() ,∴二次函数表达式为
,∴二次函数表达式为![]() ;(2)令y=0,则解得,x1=8,x2="-2" ,∴点B的坐标为(-2,0),由已知可得,在Rt△AOB中,AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∵BC=OB+OC=2+8=10,∴在△ABC中AB2+ AC2=20+80=102=BC2,∴△ABC是直角三角形;(3)由勾股定理先求出AC,AC=
;(2)令y=0,则解得,x1=8,x2="-2" ,∴点B的坐标为(-2,0),由已知可得,在Rt△AOB中,AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∵BC=OB+OC=2+8=10,∴在△ABC中AB2+ AC2=20+80=102=BC2,∴△ABC是直角三角形;(3)由勾股定理先求出AC,AC=![]() =
=![]() ,①在x轴负半轴,当AC=AN时,NO=CO=8,∴此时N(-8,0);②在x轴负半轴,当AC=NC时,NC=AC=
,①在x轴负半轴,当AC=AN时,NO=CO=8,∴此时N(-8,0);②在x轴负半轴,当AC=NC时,NC=AC=![]() ,∵CO=8,∴NO=
,∵CO=8,∴NO=![]() -8,∴此时N(8-
-8,∴此时N(8-![]() ,0);③在x轴正半轴,当AN=CN时,设CN=x,则AN=x,ON=8-x,在Rt△AON中,
,0);③在x轴正半轴,当AN=CN时,设CN=x,则AN=x,ON=8-x,在Rt△AON中,![]() +
+![]() =
=![]() ,解得:x=5,∴ON=3,∴此时N(3,0);④在x轴正半轴当AC=NC时,AC=NC=
,解得:x=5,∴ON=3,∴此时N(3,0);④在x轴正半轴当AC=NC时,AC=NC=![]() ,∴ON=
,∴ON=![]() +8,∴此时N(
+8,∴此时N(![]() +8,0);综上所述:满足条件的N点坐标是(-8,0)、(8-
+8,0);综上所述:满足条件的N点坐标是(-8,0)、(8-![]() ,0)、(3,0)、(8+
,0)、(3,0)、(8+![]() ,0);(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,∴MD∥OA,∴△BMD∽△BAO,
,0);(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,∴MD∥OA,∴△BMD∽△BAO,![]() ,∵MN∥AC,∴
,∵MN∥AC,∴![]() ,∴
,∴![]() ,∵OA=4,BC=10,BN=n+2,∴MD=
,∵OA=4,BC=10,BN=n+2,∴MD=![]() (n+2),∵S△AMN= S△ABN- S△BMN=
(n+2),∵S△AMN= S△ABN- S△BMN=![]()
=-![]() +5,∵-
+5,∵-![]() <0,∴n=3时,S有最大值,∴当△AMN面积最大时,N点坐标为(3,0).
<0,∴n=3时,S有最大值,∴当△AMN面积最大时,N点坐标为(3,0).

【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了以下不完整的统计图.

根据以上信息回答下列问题:
(1)本次共随机抽取了 名学生进行调查,听写正确的汉字个数x在 范围的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
听写正确的汉字个数x | 组中值 |
1≤x<11 | 6 |
11≤x<21 | 16 |
21≤x<31 | 26 |
31≤x<41 | 36 |
(4)该校共有1350名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.





