题目内容
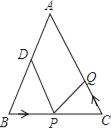
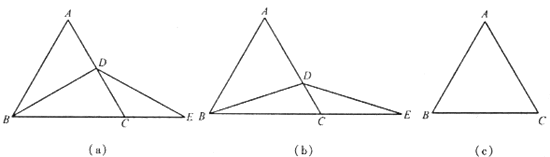
【题目】如图,分别以线段AB两端点A,B为圆心,以大于![]() AB长为半径画弧,两弧交于C,D两点,作直线CD交AB于点M,DE∥AB,BE∥CD.
AB长为半径画弧,两弧交于C,D两点,作直线CD交AB于点M,DE∥AB,BE∥CD.
(1)判断四边形ACBD的形状,并说明理由;
(2)求证:ME=AD.

【答案】(1)四边形ACBD是菱形;理由见解析;(2)证明见解析.
【解析】
(1)根据题意得出![]() ,即可得出结论;
,即可得出结论;
(2)先证明四边形![]() 是平行四边形,再由菱形的性质得出
是平行四边形,再由菱形的性质得出![]() ,证明四边形
,证明四边形![]() 是矩形,得出对角线相等
是矩形,得出对角线相等![]() ,即可得出结论.
,即可得出结论.
(1)解:四边形ACBD是菱形;理由如下:
根据题意得:AC=BC=BD=AD,
∴四边形ACBD是菱形(四条边相等的四边形是菱形);
(2)证明:∵DE∥AB,BE∥CD,
∴四边形BEDM是平行四边形,
∵四边形ACBD是菱形,
∴AB⊥CD,
∴∠BMD=90°,
∴四边形ACBD是矩形,
∴ME=BD,
∵AD=BD,
∴ME=AD.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目